10 Minute School
Log in
HomeHSC and SSC Subjects Math HSC 1st Paper Chapter 01: ম্যাট্রিক্স ও নির্ণায়ক নির্ণায়ক (Determinant)

নির্ণায়ক (Determinant)

১৬৯৩ খ্রিস্টাব্দে গণিতবিদ লিবনিজ (Leibnitz) সরল সমীকরণমালার সমাধানে এক বিশেষ সম্পর্কের অবতারণা করেন। উনবিংশ শতাব্দীতে গাউস (Gauss) এবং কসি (Cauchy) এ সম্পর্কে আরও সুস্পষ্ট ধারণা দেন। সর্বপ্রথম কসি গাণিতিক ফাংশনের নাম দেন নির্ণায়ক (Determinant).

নির্ণায়ক (Determinant):

নির্ণায়ক হলো বিশেষ আকারে লিখিত নির্দিষ্ট এক প্রকারের রাশি। কোনো বর্গ ম্যাট্রিক্স [a1a2b1b2]\begin{bmatrix} a_1 & a_2\\ b_1 & b_2 \end{bmatrix} এর উপাদানগুলোকে একই রেখে এবং তাদের অবস্থানের পরিবর্তন না করে ∣a1a2b1b2∣\begin{vmatrix} a_1 & a_2\\ b_1 & b_2 \end{vmatrix} আকারে লিখলে একে প্রদত্ত বর্গ ম্যাট্রিক্সের নির্ণায়ক বা সংক্ষেপে শুধু নির্ণায়ক বলে।

এখানে a1,a2,b1,b2a_1, a_2, b_1, b_2 কে নির্ণায়কের উপাদান এবং a1,a2a_1, a_2 হল নির্ণায়কটির প্রধান কর্ণ গঠনকারী উপাদান।

  • নির্ণায়কের উপাদানগুলোর অনুভূমিক বিন্যাসকে সারি (row) এবং উলম্ব বিন্যাসকে স্তম্ভ বা (column) বলে। 
  • নির্ণায়কের সারি ও কলাম সংখ্যা অবশ্যই সমান হতে হবে। 
  • নির্ণায়কের মাত্রা: কোন নির্ণায়কের সারি ও কলাম সংখ্যা n হলে, তাকে n মাত্রার নির্ণায়ক বলা হয়।

নির্ণায়কের পদ :

তৃতীয় মাত্রার নির্ণায়ক ∣a1b1c1a2b2c2a3b3c3∣\begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix} এর উপাদান a1,b1,c1a_1, b_1, c_1 ইত্যাদি গুণফলকে নির্ণায়কের পদ (terms) বলা হয়। 

মূখ্য কর্ণ ও মাধ্যমিক কর্ণ:

উপরের নির্ণায়ক লক্ষ্য করলে দেখা যায় a1,b2ওc3a_1, b_2 ও c_3 উপাদানগুলো একটি কর্ণ এবং a3,b2,c1a_3, b_2, c_1 উপাদানগুলো অপর একটি কর্ণ গঠন করে। প্রথম কর্ণকে মুখ্য কর্ণ এবং দ্বিতীয় কর্ণকে মাধ্যমিক কর্ণ বলা হয়। মূখ্যকর্ণের উপাদানগুলোর গুণফল a1,b2,c3a_1, b_2 , c_3 কে মুখ্যপদ এবং মাধ্যমিক কর্ণের উপাদানগুলোর গুণফলকে a3,b2,c1a_3, b_2, c_1 মাধ্যমিক পদ বলে।

নির্ণায়ক

নির্ণায়কের মান নির্ণয় (Determining of Determinant of Matrix)

এক ক্ৰমের নির্ণায়কের মান: A=[a11]A=[a_{11}] ম্যাট্রিক্সের নির্ণায়ক ∣A∣=∣a11∣=a11|A|=|a_{11}|=a_{11} 

অর্থাৎ কোনো নির্ণায়কের একটি মাত্র সারি ও একটি মাত্র কলাম থাকলে এর মান হবে নির্ণায়কটি যে সংখ্যা দ্বারা গঠিত ঐ সংখ্যাই। 

উদাহরণ: |-6|=6 আবার, |5|=5

2×2 আকারের নির্ণায়কের মান: [a11a12a21a22]\begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{bmatrix} ম্যাট্রিক্সের নির্ণায়ক ∣A∣=a11.a22−a12.a21|A|=a_{11}.a_{22}-a_{12}.a_{21}

3×3 আকারের নির্ণায়কের মান :

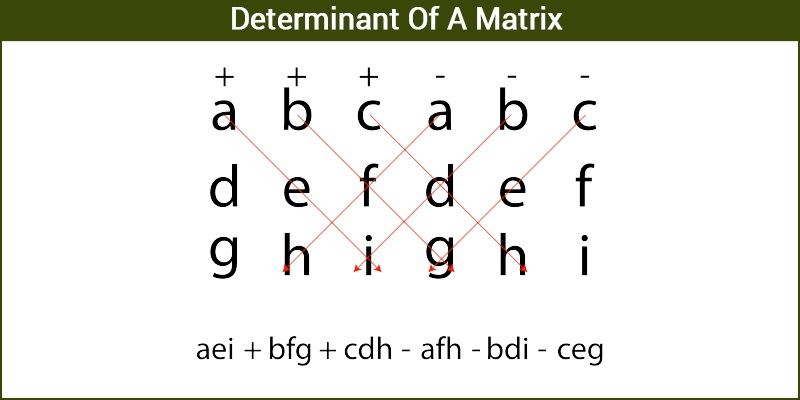
তিনটি সারি ও তিনটি কলাম দ্বারা নির্ণায়কের বিস্তার সহজে করার জন্য জন্য সারস ডায়াগ্রাম (Sarrus Diagram) ব্যবহার করা হয়। এ পদ্ধতিতে নির্ণায়কের ভুক্তিগুলিকে পাশাপাশি দুইবার লিখে নির্ণায়কের মান নিম্নোক্তভাবে বের করা হয়।  

A=[a11a12a13a21a22a23a31a32a33]A=\begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{bmatrix} ম্যাট্রিক্সের নির্ণায়ক  

∣A∣=a11a22a33+a12a23a31+a13a21a32−a11a23a32−a12a23a31−a13a22a31......(i)=a11(a22a33−a23a32)+a12(a21a33−a23a31)+a13(a21a32−a22a31)=a11∣a22a23a32a33∣−a12∣a21a23a31a32∣+a13∣a21a22a31a32∣......(ii)|A|=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32}-a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}......(i)\\ = a_{11}(a_{22}a_{33}-a_{23}a_{32})+a_{12}(a_{21}a_{33}-a_{23}a_{31})+a_{13}(a_{21}a_{32}-a_{22}a_{31})\\ =a_{11}\begin{vmatrix} a_{22} & a_{23}\\ a_{32} & a_{33} \end{vmatrix}-a_{12}\begin{vmatrix} a_{21} & a_{23}\\ a_{31} & a_{32} \end{vmatrix}+a_{13}\begin{vmatrix} a_{21} & a_{22}\\ a_{31} & a_{32} \end{vmatrix}......(ii)

 

অন্যভাবে (ii) হতে বলা যায় {(1,1)–তম ভুক্তি ×(১ম সারি ও ১ম কলাম বাদে অবশিষ্ট অংশের নির্ণায়ক)}-{(1,2)–তম ভুক্তি ×(১ম সারি ও ২য় কলাম বাদে অবশিষ্ট অংশের নির্ণায়ক)}+{(1,3)–তম ভুক্তি ×(১ম সারি ও ৩য় কলাম বাদে অবশিষ্ট অংশের নির্ণায়ক)} সরল করলে তিন ধরনের নির্ণায়ক পাওয়া যায়। 

দ্রষ্টব্য:

  • উল্লিখিত নিয়ম অনুসারে যেকোনো সারি বা কলাম বরাবর বিস্তৃতি করলেও নির্ণায়কের মান একই পাওয়া যাবে।
  • এখানে শুধুমাত্র প্রথম সারি বরাবর বিস্তৃতি দেখানো হয়েছে, যেকোনো সারি বা কলাম বরাবর বিস্তৃতি করার নিয়ম নিম্নরূপ : নির্ণায়ক = নির্দিষ্ট সারি বা কলামের {(১ম চিহ্নযুক্ত ভুক্তি) (ভুক্তিটি ধারণকারী সারি ও কলাম ব্যতীত অবশিষ্ট নির্ণায়ক)} + {(২য় চিহ্নযুক্ত ভুক্তি) (ভুক্তিটি ধারণকারী সারি ও কলাম ব্যতীত অবশিষ্ট নির্ণায়ক)}+ {(৩য় চিহ্নযুক্ত ভুক্তি) (ভুক্তিটি ধারণকারী সারি ও কলাম ব্যতীত অবশিষ্ট নির্ণায়ক)}

(p,q)– তম ভুক্তির চিহ্ন =(−1)p+q(-1)^{p+q}

উপরি-উক্ত নির্ণায়কটিকে তৃতীয় সারি বরাবর বিস্তৃতি করলে, 

∣21105−21−34∣=(−1)3+1(1)∣115−2∣+(−1)3+2(−3)∣210−2∣+(−1)3+3(4)∣2105∣=(−2−5)+3(−4)+4×10+−7−12+40=21\begin{vmatrix} 2 & 1 & 1\\ 0 & 5 & -2\\ 1 & -3 & 4 \end{vmatrix}=(-1)^{3+1}(1)\begin{vmatrix} 1 & 1\\ 5 & -2 \end{vmatrix}+(-1)^{3+2}(-3)\begin{vmatrix} 2 & 1\\ 0 & -2 \end{vmatrix}+(-1)^{3+3}(4)\begin{vmatrix} 2 & 1\\ 0 & 5 \end{vmatrix}\\ =(-2-5)+3(-4)+4\times 10+-7-12+40=21

আবার দ্বিতীয় কলাম বরাবর বিস্তৃতি করলে, 

∣21105−21−34∣=(−1)1+2(1)∣0−214∣+(−1)2+2(5)∣2114∣+(−1)3+2(−3)∣210−2∣=−(2)+5(8−1)+3(−4)=−2+35−12=21\begin{vmatrix} 2 & 1 & 1\\ 0 & 5 & -2\\ 1 & -3 & 4 \end{vmatrix}=(-1)^{1+2}(1)\begin{vmatrix} 0 & -2\\ 1 & 4 \end{vmatrix}+(-1)^{2+2}(5)\begin{vmatrix} 2 & 1\\ 1 & 4 \end{vmatrix}+(-1)^{3+2}(-3)\begin{vmatrix} 2 & 1\\ 0 & -2 \end{vmatrix}\\ =-(2)+5(8-1)+3(-4)=-2+35-12=21

 

নির্ণায়কের অনুরাশি এবং সহগুণক (Minor and Cofactor of Determinant)

কোনো নির্ণায়ক D এর কোনো ভুক্তি যে সারি ও যে কলামে অবস্থিত সে সারি ও সে কলাম ব্যতীত অবশিষ্ট ভুক্তি দ্বারা গঠিত নির্ণায়ককে উক্ত ভুক্তির অনুরাশি বলা হয়। 

যেমন: ∣a11a12a13a21a22a23a31a32a33∣\begin{vmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{vmatrix} নির্ণায়কের a11,a12,a13a_{11},a_{12},a_{13} এর অর্থাৎ (1,1), (1,2), (1,3)–তম অনুরাশি যথাক্রমে ∣a22a23a32a33∣,∣a21a23a31a33∣,∣a21a22a31a32∣\begin{vmatrix} a_{22} & a_{23}\\ a_{32} & a_{33} \end{vmatrix}, \begin{vmatrix} a_{21} & a_{23}\\ a_{31} & a_{33} \end{vmatrix}, \begin{vmatrix} a_{21} & a_{22}\\ a_{31} & a_{32} \end{vmatrix}

যথাযথ চিহ্নযুক্ত কোনো ভুক্তির অনুরাশিকে সে ভুক্তির সহগুণক বলা হয়। কোনো নির্ণায়কের (r,c)–তম সহগুণকের চিহ্ন হবে (−1)r+c(-1)^{r+c} অর্থাৎ (r+c) জোড় হলে ‘+’ চিহ্ন এবং বিজোড় হলে ‘−’ চিহ্ন হবে। তৃতীয় মাত্রার নির্ণায়কের চিহ্ন ∣+−+−+−+−+∣\begin{vmatrix} + & - & +\\ - & + & -\\ + & - & + \end{vmatrix} অর্থাৎ কোণাকোণি অবস্থিত উপাদান ৫টি চিহ্ন ‘+’ এবং অপর ৪টির চিহ্ন ‘−’  

সহগুণকের চিহ্ন সনাক্তকরণ:

কোন নির্ণায়কের যে উপাদানের সহগুণক বের করতে হলে উক্ত উপাদানটি যত নং কলাম ও যত নং সারিতে আছে তাদের যোগফল জোড় সংখ্যা হলে, সহগুণকের চিহ্ন ধনাত্মক (+ve) হবে এবং যোগফল বিজোড় হলে, চিহ্ন ঋণাত্মক (-ve) হবে। 

নির্ণায়কের বিস্তৃতি :

নির্ণায়কের বিস্তৃতি বুঝানোর জন্য তৃতীয় ক্রমের একটি নির্ণায়ক বিবেচনা করি।

D=∣a1b1c1a2b2c2a3b3c3∣D=\begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix} নির্ণায়কটিকে প্রথম কলাম বরাবর বিস্তার করি। এ জন্য a1a_1 বরাবর কলাম ও সারি বাদ দিলে বাকি চারটি উপাদান নিয়ে একটি 2×2 ক্ৰমের নির্ণায়ক হয়, যা a1a_1 এর সাথে গুণ করি। এরপর প্রথম কলাম এর দ্বিতীয় উপাদন a2a_2 নিয়ে পূর্বের নিয়মে a2a_2 বরাবর কলাম ও সারি বাদ দিলে বাকি চারটি উপাদন দিয়ে একটি 2×2 ক্ৰমের নির্ণায়ক হয়, যার পূর্বে একটা ঋণাত্মক চিহ্ন দিয়ে a2a_2 এর সাথে গুণ করি এবং সব শেষে প্রথম কলামের শেষ বা তৃতীয় উপাদন a3a_3 নিয়ে পূর্বের নিয়মে প্রাপ্ত 2×2 ক্রমের নির্ণায়কের সাথে a3 গুণ করি। প্রাপ্ত মানগুলিই হচ্ছে নির্ণায়কটির চূড়ান্ত বিস্তৃতি। নিচে তা দেখান হল: 

D=a1∣b2b3c2c3∣−a2∣b1c1b3c3∣+a3∣b1c1b2c2∣=a1(b2c3−b3c2)−a2(c3b1−b3c1)+a3(b1c2−b2c1)=(a1b2c3+b1c2a3+c1a2b3)−(a3b2c1+b3c2a1+c3a2b1)D=a_1\begin{vmatrix} b_2 & b_3\\ c_2 & c_3 \end{vmatrix}-a_2\begin{vmatrix} b_1 & c_1\\ b_3 & c_3 \end{vmatrix}+a_3\begin{vmatrix} b_1 & c_1\\ b_2 & c_2 \end{vmatrix}\\ =a_1(b_2c_3-b_3c_2)-a_2(c_3b_1-b_3c_1)+a_3(b_1c_2-b_2c_1)\\ =(a_1b_2c_3+b_1c_2a_3+c_1a_2b_3)-(a_3b_2c_1+b_3c_2a_1+c_3a_2b_1)

 

 

এইচএসসি ও এডমিশন পরীক্ষার্থীদের জন্য আমাদের কোর্সসমূহঃ

 

আমাদের স্কিল ডেভেলপমেন্ট কোর্সসমূহঃ

 

১০ মিনিট স্কুলের ক্লাসগুলো অনুসরণ করতে ভিজিট: www.10minuteschool.com

Other Topics