10 Minute School
Log in
HomeHSC and SSC Subjects Math HSC 1st Paper Chapter 09: অন্তরীকরণ (Differentiation) লিমিটের সূত্র (Limit formula) 

লিমিটের সূত্র (Limit formula) 

অন্তরীকরণ সূত্র: লিমিট (Limit formula) 

যেন তেন প্রকারেন ( যেকোনো উপায় ) অসং জ্ঞায়িত অবস্থায় দূর করতে হবে।

প্রয়োজনীয় কিছু ধারা (Some necessary sections) 

  • (1+x)n(1+x)^{n} =1+nx+n(n−1)2!x2+n(n−1)(n−2)3!x3+−−−−−−−1+n x+\frac{n(n-1)}{2 !} \mathrm{x}^{2}+\frac{\mathrm{n}(\mathrm{n}-1)(n-2)}{3 !} x^{3}+-------
  • exe^{x} =1+x+x22!+x33!+x44!+1+x+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+\frac{x^{4}}{4 !}+
  • ln⁡(1+x)\ln (1+x) =x−x22+x33−x44+−−−−−−x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\frac{x^{4}}{4}+------
  • ln⁡(1−x)\ln (1-x) =−x−x22−x33−x44−−−−−−−-x-\frac{x^{2}}{2}-\frac{x^{3}}{3}-\frac{x^{4}}{4}-------
  • e−xe^{-x} =1−x+x22!−x33!+x44!− - - - - - - - 1-x+\frac{x^{2}}{2 !}-\frac{x^{3}}{3 !}+\frac{x^{4}}{4 !}-\text { - - - - - - - }
  • axa^{x} =1+xln⁡a+x22!(ln⁡a)2+x33!(ln⁡a)3+−−−−−−−−−−1+x \ln a+\frac{x^{2}}{2 !}(\ln a)^{2}+\frac{x^{3}}{3 !}(\ln a)^{3}+----------
  • a−xa^{-x} =1−xln⁡a+x22!(ln⁡a)2−x33!(ln⁡a)3+−−−−−−−1-x \ln a+\frac{x^{2}}{2 !}(\ln a)^{2}-\frac{x^{3}}{3 !}(\ln a)^{3}+-------

বিশেষ কিছু ফাংশনের সীমা নির্ণয় (Determining the limits of certain functions) :

 1. tin⁡iix→0ex−1x=1\text { 1. } \frac{\operatorname{tin}_{i i}}{x \rightarrow 0} \frac{e^{x}-1}{x}=1

প্রমানঃ           exe^{x}=1+x+x22!+x33!+−−−−−−−1+x+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+-------

∴lim⁡x→0ex−1x\therefore \frac{\lim }{x \rightarrow 0} \frac{e^{x}-1}{x} =lim⁡x→01x{(1+x+x22!+x33!+−−−−)−1}\frac{\lim }{x \rightarrow 0} \frac{1}{x}\left\{\left(1+x+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+----\right)-1\right\}

=lim⁡x→01x{x+x22!+x32!+−−−}=\frac{\lim }{x \rightarrow 0} \frac{1}{x}\left\{x+\frac{x^{2}}{2 !}+\frac{x^{3}}{2 !}+---\right\}  

=lim⁡x→01x⋅x{1+x22!+x33!+−−−}=\frac{\lim }{x \rightarrow 0} \frac{1}{x} \cdot x\left\{1+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+---\right\}

=1=1  [Proved]

 2. lim⁡x→0sin⁡xx=1\text { 2. } \frac{\lim }{x \rightarrow \mathbb{0}} \frac{\sin x}{x}=1

প্রমানঃ 

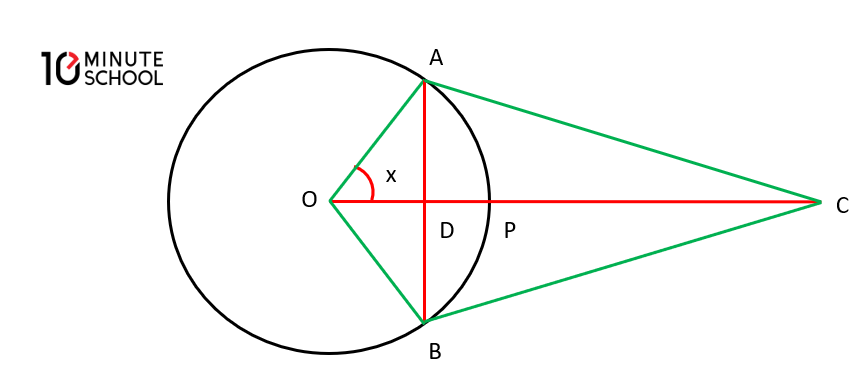
অন্তরীকরণ সূত্র
এখানে-

APB চাপ

OP ব্যাসার্ধ

A ও B বিন্দুতে অঙ্কিত  স্পর্শক OP এর বর্ধিতাংশকে c বিন্দুতে পরস্পরকে ছেদ করে।

<P0A=xx রেডিয়ান

এখন-

জ্যা AB < চাপ APB  < AC + BC

⟹2AD < 2 চাপ AP < 2AC

⟹AD < চাপ AP <AC

⟹ADOA\frac{A D}{O A} <চাপ APOA\frac{\text {চাপ } A P}{O A} <ACOA\frac{A C}{O A}

⟹sin⁡x\sin x <xx <tanx−−−−−−−−1tan x--------1

⟹1<xsin⁡x\frac{x}{\sin x} <1cos⁡x\frac{1}{\cos x}

⟹cos⁡x\cos x <sin⁡xx\frac{\sin x}{x} <1

x→0x \rightarrow 0 হলে,cos⁡x→1\cos x \rightarrow 1

⟹lim⁡x→0\frac{\lim }{x \rightarrow 0} cos⁡x\cos x <lim⁡x→0\frac{\lim }{x \rightarrow 0} sin⁡xx\frac{\sin x}{x} <1

⟹1<lim⁡x→0\frac{\lim }{x \rightarrow 0} sin⁡xx\frac{\sin x}{x} <1

∴lim⁡x→0\frac{\lim }{x \rightarrow 0} sin⁡xx\frac{\sin x}{x} =1

[Proved]

 

3.ln⁡iii x→0tar⁡xx=1\frac{\ln _{\text {iii }}}{x \rightarrow 0} \frac{\operatorname{tar} x}{x}=1

প্রমানঃ 

(1) হতে পাই –

sin⁡x\sin x < xx < tan⁡x\tan x

⟹cos⁡x\cos x < xtan⁡x\frac{x}{\tan x} < 1

⟹lim⁡x→0\frac{\lim }{x \rightarrow 0} cos⁡x\cos x <lim⁡x→0\frac{\lim }{x \rightarrow 0} xtan⁡x\frac{x}{\tan x} <1

⟹1<lim⁡x→0\frac{\lim }{x \rightarrow 0} xtan⁡x\frac{x}{\tan x} <1

∴lim⁡x→0\frac{\lim }{x \rightarrow 0} xtan⁡x\frac{x}{\tan x} =1

[Proved]

 

4.lim⁡x→0\frac{\lim }{x \rightarrow 0} ln⁡(1+x)x\frac{\ln (1+x)}{x} =1

প্রমানঃ 

lim⁡x→0\frac{\lim }{x \rightarrow 0} ln⁡(1+x)x\frac{\ln (1+x)}{x} =lim⁡x→01x\frac{\lim }{x \rightarrow 0} \frac{1}{x} (x−x22+x33+x44+−−−−)\left(x-\frac{x^{2}}{2}+\frac{x^{3}}{3}+\frac{x^{4}}{4}+----\right)

=lim⁡x→0\frac{\lim }{x \rightarrow 0} 1x\frac{1}{x} .xx (1−x22+x33−x44+−−−−−)\left(1-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\frac{x^{4}}{4}+-----\right)

=1

[Proved]

 

5.lim⁡x→0\frac{\lim }{x \rightarrow 0} xn−anx−a\frac{{x^{n}-a^{n}}}{x-a} =nan−1n a^{n}-1

প্রমানঃ 

ধরি, x=a+h;h→0x=a+h ; h \rightarrow 0 যখন x→ax \rightarrow a

lim⁡x→axn−anx−a=lim⁡h→0(a+h)n−ana+h−a\frac{\lim }{x \rightarrow a} \frac{x^{n}-a^{n}}{x-a}=\frac{\lim }{h \rightarrow 0} \frac{(a+h)^{\mathrm{n}}-a^{\mathrm{n}}}{a+h-a} =lim⁡h→0(a+h)n−anh=lim⁡h→01h{an(1+ha)n−an}=lim⁡h→0anh{(1+ha)n−1}=lim⁡h→0anh{1+nha+n(n−1)2!h2a2+n(n−1)(n−2)3!h3a3+−−−−−1}=lim⁡h→0anh⋅nha{1+(n−1)2!ha+n(n−1)(n−2)3!h2a2+−−−}=nana=nan−1\begin{array}{l} =\frac{\lim }{h \rightarrow 0} \frac{(\mathrm{a}+\mathrm{h})^{\mathrm{n}}-\mathrm{a}^{\mathrm{n}}}{\mathrm{h}} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h}\left\{a^{n}\left(1+\frac{h}{a}\right)^{n}-a^{n}\right\} \\ =\frac{\lim }{h \rightarrow 0} \frac{a^{n}}{h}\left\{\left(1+\frac{h}{a}\right)^{n}-1\right\} \\ =\frac{\lim }{h \rightarrow 0} \frac{a^{n}}{h}\left\{1+\frac{n h}{a}+\frac{n(n-1)}{2 !} \frac{h^{2}}{a^{2}}+\frac{n(n-1)(n-2)}{3 !} \frac{h^{3}}{a^{3}}+-----1\right\} \\ =\frac{\lim }{h \rightarrow 0} \frac{a^{n}}{h} \cdot \frac{n h}{a}\left\{1+\frac{(n-1)}{2 !} \frac{h}{a}+\frac{n(n-1)(n-2)}{3 !} \frac{h^{2}}{a^{2}}+---\right\} \\ =\frac{n a^{n}}{a}=n a^{n-1} \end{array}

[Proved]

⟹ একনজরে সব সূত্রঃ

  • lim⁡x→0sin⁡xx=1\frac{\lim }{x \rightarrow 0} \frac{\sin x}{x}=1
  • lim⁡x→0xsin⁡x=1\frac{\lim }{x \rightarrow 0} \frac{x}{\sin x}=1
  • lim⁡x→0tan⁡xx=1\frac{\lim }{x \rightarrow 0} \frac{\tan x}{x}=1
  • lim⁡x→0xtan⁡x=1\frac{\lim }{x \rightarrow 0} \frac{x}{\tan x}=1
  • lim⁡x→0ex−1x=1\frac{\lim }{x \rightarrow 0} \frac{e^{x}-1}{x}=1
  • lim⁡x→0ln⁡(1+x)x=1\frac{\lim }{x \rightarrow 0} \frac{\ln (1+x)}{x}=1
  • lim⁡x→0(1+x)n−1x=n\frac{\lim }{x \rightarrow 0} \frac{(1+x)^{n}-1}{x}=n
  • lim⁡x→0xn−anx−a=nan−1\frac{\lim }{x \rightarrow 0} \frac{x^{n}-a^{n}}{x-a}=n a^{n-1}
  • lim⁡x→0(1+x)1x=e\frac{\lim }{x \rightarrow 0}(1+x)^{\frac{1}{x}}=e
  • lim⁡x→∞(1+1x)x=e\frac{\lim }{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^{x}=e

এইচএসসি ও এডমিশন পরীক্ষার্থীদের জন্য আমাদের কোর্সসমূহঃ

 

আমাদের স্কিল ডেভেলপমেন্ট কোর্সসমূহঃ

 

১০ মিনিট স্কুলের ক্লাসগুলো অনুসরণ করতে ভিজিট: www.10minuteschool.com

Other Topics