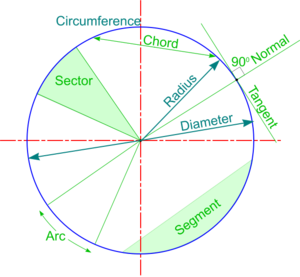
বৃত্তের স্পর্শক ও অভিলম্ব (Tangent and Normal of a circle)

বৃত্তের স্পর্শক কাকে বলে? (Tangent of a circle):

মনে করি, $PQ$ সরলরেখা একটি বৃত্তকে $P,Q$ বিন্দুতে ছেদ করেছে। যদি $PQ$ সরলরেখাটিকে $P$ বিন্দুতে স্থির রেখে $B$ বিন্দুকে বৃত্তের পরিধি বরাবর এমনভাবে ঘুরাই যেন $Q$ বিন্দু ক্রমশ $P$ বিন্দুর নিকটবর্তী হয়ে সবশেষে $P$ বিন্দুতে সমাপতিত হয়ে স্থির হয় তবে সর্বশেষ সরলরেখাটি $P$ বিন্দুতে বৃত্তটির স্পর্শক হবে।

কোনো সরলরেখা একটি বৃত্তকে দুইটি সমাপতিত বিন্দুতে ছেদ করলে সরলরেখাটিকে বৃত্তটির ঐ বিন্দুকে স্পর্শক বলে। চিত্রে $PT$ স্পর্শক।

যে বিন্দুতে স্পর্শকটি বক্ররেখাটির সাথে মিলিত হয় তাকে স্পর্শ বিন্দু (Point of Contact) বলে। চিত্রে $P$ হল স্পর্শবিন্দু।

বৃত্তের স্পর্শকের বৈশিষ্ট্য (Properties of a Tangent of a circle):

বৃত্তের স্পর্শকের কয়েকটি বৈশিষ্ট্য আছে যার এ অধ্যায়ে প্রায়োগিক গুরুত্ব আছে। যেমন –

বৃত্তের কেন্দ্র ও স্পর্শবিন্দুর দূরত্ব বৃত্তের ব্যাসার্ধের সমান।
বৃত্তের কেন্দ্র ও স্পর্শবিন্দুর সংযোজক রেখা স্পর্শকের উপর লম্ব হয়।
বৃত্তের স্পর্শক বৃত্তটিকে স্পর্শবিন্দু ভিন্ন অপর কোনো বিন্দুতে ছেদ করে না।

বৃত্তের অভিলম্ব (Normal of a circle):

বৃত্তের কোনো স্পর্শকের স্পর্শবিন্দুতে স্পর্শকের উপর লম্বরেখাকে অভিলম্ব বলে। চিত্রে $PO$ অভিলম্ব। কোন বৃত্তের অভিলম্ব এর কেন্দ্র বিন্দু দিয়ে যায়।

বৃত্তের স্পর্শক ও অভিলম্বের সমীকরণ (Equation of Tangent and normal to a circle):

$x^2+y^2+2gx+2fy+c=0$ বৃত্তের উপরিস্থিত $P(x_1,y_1)$ বিন্দুতে অঙ্কিত স্পর্শকের সমীকরণ, $xx_1+yy_1+g(x+x_1)+f(y+y_1)+c=0$

$x^2+y^2+2gx+2fy+c=0......(1)$ বৃত্তটির কেন্দ্র $O(-g, -f)$ এবং ব্যাসার্ধ = $\sqrt{g^2+f^2-c}$

$P(x_1,y_1)$ বিন্দুটি (1) বৃত্তের উপর অবস্থিত বলে,

x_1^2+y_1^2+2gx_1+2fy_1+c=0......(2)

ধরি স্পর্শকটির উপর যেকোনো একটি বিন্দু $Q(x, y)$ ।

$OP$ এর ঢাল = $\frac{y_1+f}{x_1+g}$ এবং $PQ$ এর ঢাল = $\frac{y-y_1}{x-x_1}$

$P(x_1,y_1)$ বিন্দুতে (1) বৃত্তটির স্পর্শক $PQ$ বলে, $OP\perp PQ$

\therefore \frac{y_1+f}{x_1+g}\times \frac{y-y_1}{x-x_1}=-1\\ \Rightarrow yy_1-y_1^2+fy-fy_1=-(xx_1-x_1^2+gx-gx_1)\\ \Rightarrow yy_1-y_1^2+fy-fy_1=-xx_1+x_1^2-gx+gx_1\\ \Rightarrow xx_1+yy_1+gx+gx_1+fy+fy_1+c=x_1^2+y_1^2+2gx_1+2fy_1+c\\ \therefore xx_1+yy_1+gx+gx_1+fy+fy_1+c=0 [(2) হতে]

এ সমীকরণকে লেখা যায়, $xx_1+yy_1+gx+2g\frac{x+x_1}{2}+2f\frac{y+y_1}{2}+c=0$

বি.দ্র.: যেকোনো দ্বিঘাত সমীকরণে (বৃত্ত, পরাবৃত্ত, উপবৃত্ত, অধিবৃত্ত ইত্যাদি) $x^2$ এর স্থলে $xx_1, y^2$ এর স্থলে $yy_1, x$ এর স্থলে $\frac{x+x_1}{2}$ এবং $y$ এর স্থলে $\frac{y+y_1}{2}$ বসালে, $(x_1,y_1)$ বিন্দুতে স্পর্শকের সমীকরণ পাওয়া যায়।

অভিলম্ব (Normal of a circle):

কোনো বৃত্তের স্পর্শ বিন্দুগামী স্পর্শকের উপর লম্ব রেখাকে ঐ বৃত্তের অভিলম্ব বলা হয়।

মনে করি, $x^2+y^2=r^2$ বৃত্তের উপর $(x_1,y_1)$ যে কোনো একটি বিন্দু।

$(x_1,y_1)$ বিন্দুতে বৃত্তের স্পর্শকের সমীকরণ, $xx_1+yy_1=r^2......(1)$

$(x_1,y_1)$ বিন্দুগামী $(1)$ সরলরেখার উপর লম্বরেখার সমীকরণ, $xy_1-yx_1=x_1y_1-x_1y_1$

$x_1y-y_1x=0$ এটিই অভিলম্বের সমীকরণ।

অনুরূপভাবে, $(x_1,y_1)$ বিন্দুতে $x^2+y^2+2gx+2fy+c=0$ বৃত্তের অভিলম্বের সমীকরণ, $(y_1+f)x-(x_1+g)y+gy_1-fx_1=0$

বি.দ্র.:

অভিলম্বের সূত্রটি পরাবৃত্ত, অধিবৃত্ত, উপবৃত্ত এর জন্যও প্রযোজ্য।
বৃত্তের অভিলম্ব কেন্দ্রগামী হয়।

$y=mx+c$ রেখাটি $x^2+y^2=r^2$ বৃত্তের স্পর্শক হওয়ার শর্ত:

যেহেতু $x^2+y^2=r^2$ বৃত্তে $(x_1,y_1)$ বিন্দুতে স্পর্শকের সমীকরণ,

xx_1+yy_1=r^2......(1)

সুতরাং $y=mx+c$

বা, $-mx+y=c......(2)$

রেখাটি বৃত্তের স্পর্শক হলে (1) ও (2) অভিন্ন।

\therefore \frac{x_1}{-m}=\frac{y_1}{1}=\frac{r^2}{c}\\ \Rightarrow x_1=-\frac{mr^2}{c},y_1=\frac{r^2}{c}

$\therefore (x_1,y_1)$ বিন্দুটি (2) নং রেখার উপর অবস্থিত। সুতরাং, $(x_1,y_1)$ সমীকরণ (2) কে সিদ্ধ করবে।

অতএব, $y_1=mx_1+c\\ \Rightarrow \frac{r^2}{c}=-\frac{m^2r^2}{c}+c [x_1,y_1\; এর\; মান\; বসিয়ে]\\ \Rightarrow r^2=-m^2r^2+c^2 [c\; দিয়ে\; গুণ\; করে]\\ \Rightarrow c^2=r^2(1+m^2)\\ \therefore c= \pm r\sqrt{1+m^2}$

সুতরাং, $y=mx+c$ রেখাটি $x^2+y^2=r^2$ বৃত্তের স্পর্শক হওয়ার শর্ত: $c=\pm r\sqrt{1+m^2}$

অনুসিদ্ধান্ত-১: $m$ এর সকল মানের জন্য $y=mx\pm r\sqrt{1+m^2}$ রেখাটি $x^2+y^2=r^2$ বৃত্তের স্পর্শক হবে।

অনুসিদ্ধান্ত-২: $y=mx+c$ রেখাটি $x^2+y^2=r^2$ বৃত্তকে স্পর্শ করলে, স্পর্শবিন্দুর স্থানাঙ্ক $\Big(\frac{-mr}{\sqrt{1+m_2}}, \frac{r}{\sqrt{1+m_2}} \Big)$

প্রমাণ:

x_1=-\frac{mr_2}{c}=-\frac{mr^2}{r\sqrt{1+m^2}}=-\frac{mr}{\sqrt{1+m^2}} [\because c=\pm r\sqrt{1+m^2}]\\ y_1=\frac{r^2}{c}=\frac{r^2}{r\sqrt{1+m^2}}=\frac{r}{1+m^2} [\because c=\pm r\sqrt{1+m^2}]

এইচএসসি ও এডমিশন পরীক্ষার্থীদের জন্য আমাদের কোর্সসমূহঃ

আমাদের স্কিল ডেভেলপমেন্ট কোর্সসমূহঃ

১০ মিনিট স্কুলের ক্লাসগুলো অনুসরণ করতে ভিজিট: www.10minuteschool.com

Other Topics