রাসায়নিক সাম্যাবস্থা (Chemical equilibrium)
প্রশ্নঃ রাসায়নিক সাম্যাবস্থা বলতে কী বুঝ (Chemical equilibrium)?
উত্তরঃ
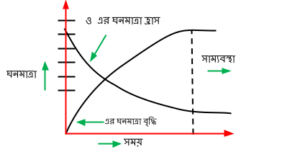
যে অবস্থায় কোনো উভমূখী বিক্রিয়ার সম্মূখ ও পশ্চাৎমূখী বিক্রিয়ার হার সমান হয় এবং বিক্রিয়ক ও উৎপাদের ঘনমাত্রার আর কোনো পরিবর্তন হবে না, তাকে রাসায়নিক সাম্যবস্থা বলা হয়। এ বিষয়টিকে নিম্নের লেখচিত্রের মাধ্যমে দেখানো হল-
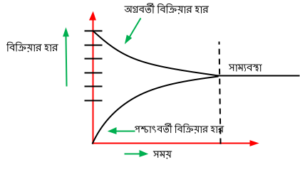
সাম্যাবস্থায় H_{2} ও I_{1} থেকে H I এর সৃষ্টি এবং H I এর বিয়োজন থেকে H_{2} ও I_{1} এর সৃষ্টি সমহারে চলে।
প্রশ্নঃ রাসায়নিক সাম্যাবস্থা একটি গতিশীল অবস্থা, ব্যাখ্যা কর। (Chemical equilibrium is a dynamic state)
উত্তরঃ
সাম্যবস্থায় কোনো বিক্রিয়া আপাতদৃষ্টিতে বন্ধ বলে মনে হলেও প্রকৃতপক্ষে সম্মুখমূখী ও পশ্চাৎমূখী উভয় বিক্রিয়া সমান গতিতে চলতে থাকে। তাই আপাতদৃষ্টিতে সাম্যবস্থাকে স্থির বলে মনে হলে, এটি একটি গতিশীল অবস্থা যা নিম্নের পরীক্ষালব্ধ প্রমাণ হতে পাওয়া যায় । নির্দিষ্ট তাপমাত্রায় একটি আবদ্ধ পাত্রে H_{2} এবং গাঢ় বেগুনী বর্ণের I_{2} বাষ্প নিয়ে রেখে দিলে প্রথম দিকে H_{2} ও I_{2} এর ঘনমাত্রা বেশি হওয়ায় দ্রুত হারে \mathrm{HI} উৎপন্ন হতে থাকে। এ বিক্রিয়ার হার কমতে থাকে এবং পশ্চাৎমূখী বিক্রিয়ার হার অর্থাৎ, \mathrm{HI} এর বিয়োজন হার বৃদ্ধি পেতে থাকে। একসময় মিশ্রণের বর্ণ হালকা বেগুনী হওয়ার পর বর্ণের আর কোন পরিবর্তন হয় না। অর্থাৎ, তখন বিক্রিয়াটি সাম্যবস্থায় পৌছেছে। সাম্যবস্থা অর্জনের পর ট্রেসার বা শণাক্তকারী হিসেবে তেজস্ক্রিয় \frac{128}{53} l^{*} যোগ করা হলে দেখা যায় যে, কিছুক্ষণ পর উৎপন্ন \mathrm{HI} এর I_{2} তেজস্ক্রিয় হয় এবং এ ধরনের \mathrm{HI}^{*} এর পরিমাণ ক্রমশ বাড়তে থাকে । \mathrm{H}_{2}+\mathrm{I}_{2} * \rightarrow 2 \mathrm{HI} * যেহেতু, সাম্যবস্থায় \mathrm{HI} এর সর্বমোট পরিমাণ প্রায় অপরিবর্তিত থাকে। তাই \mathrm{HI}^{*} উৎপন্ন হওয়ার সময় এর সাথে কিছু অতেজস্ক্রিয় \mathrm{HI} বিয়োজিত হয়ে H_{2} ও I_{2}এ পরিণত হয়।
2 H I \rightarrow H_{2}+I_{2}
অর্থাৎ, উপরোক্ত পরীক্ষা থেকে বলা যায়, সাম্যবস্থা একটি গতিশীল অবস্থা, স্থির অবস্থা নয়।
প্রশ্নঃ সব রাসায়নিক বিক্রিয়া সাম্যাবস্থায় দিকে ধাবমান- ব্যাখ্যা কর। (All chemical reactions are running towards equilibrium)
উত্তরঃ
বিভিন্ন বিক্রিয়ার গতিবেগ থেকে বলা যায় যে, সব রাসায়নিক বিক্রিয়া সাম্যবস্থার দিকে ধাবমান। সব রাসায়নিক বিক্রিয়া উভমূখী বিক্রিয়ায় পরিণত হয়ে সাম্যবস্থায় পৌছে। যেমন ইথানল \left(\mathrm{CH}_{2} \mathrm{CH}_{2} \mathrm{OH}\right) এবং ইথানয়িক এসিডের \left(\mathrm{CH}_{3} \mathrm{COOH}\right) সমমোলার পরিমাণ মিশ্রিত করে প্রায় 100°C তাপমাত্রায় দীর্ঘক্ষণ রাখা হলে দেখা যায় যে, এরা বিক্রিয়া করে ইথাইল-ইথানয়েট ও পানি উৎপন্ন করে। বিক্রিয়া চলতে থাকে, বিক্রিয়কের পরিমাণ হ্রাস পাবে এবং উৎপাদের পরিমাণ বৃদ্ধি পাবে । কিন্তু 66.7% ইথানল এবং 66.7% ইথানয়িক এসিড বিক্রিয়া করে 66.7% ইথাইল ইথানয়েট এবং 66.7% পানি উৎপন্ন হওয়ার পর বিক্রিয়ক এবং উৎপাদের পরিমাণের আর কোনো পরিবর্তন হয় না যা থেকে বোঝা যায়, বিক্রিয়াটি সাম্যাবস্থার দিকে ধাবমান।
\begin{array}{lcccc} & \mathrm{CH}_{3} \mathrm{COOH} & + \mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH} & \rightarrow & \mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{3} & + \mathrm{H}_{2} \mathrm{O} \\ \text { বিক্রিয়ার শুরুতে: } & 100 \% & 100 \% && 0 \% & 0 \% \\ \text { একটি নির্দিষ্ট সময় পর, } & 33.3 \% & 33.3 \% && 66.7 \% & 66.7 \% \end{array}আবার, সমমোলার ইথাইল ইথানয়েট এবং পানি নিয়ে 100°C তাপমাত্রায় রেখে দিলে ইথানল এবং ইথানয়িক এসিড উৎপন্ন হয়। কিন্তু বিক্রিয়কের পরিমাণ 66.7% এ পৌছানোর পর আর কোনো উৎপাদ উৎপন্ন হয় না।
\begin{array}{lcccc} \text { বিক্রিয়া : } & \mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{3} & + \mathrm{H}_{2} \mathrm{O} & \rightarrow & \mathrm{CH}_{3} \mathrm{COOH} & + \mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH} \\ \text { বিক্রিয়ার শুরুতে: } & 100 \% & 100 \% && 0 \% & 0 \% \\ \text { একটি নির্দিষ্ট সময় পর, } & 66.7 \% & 66.7 \% && 33.3 \% & 33.3 \% \end{array}শুধু সমমোলার নয় যেকোনো পরিমাণ বিক্রিয়ক উৎপাদ নিয়ে দেখা যায়, বিক্রিয়াটি সমাপ্তির দিকে বরং সাম্যাবস্থার দিকে ধাবমান। তাই বিক্রিয়াটিকে নিম্নরূপে লেখা যায়-
\mathrm{CH}_{3} \mathrm{COOH}+\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH} \rightleftharpoons \mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{3}+\mathrm{H}_{2} \mathrm{O}
প্রশ্নঃ রাসায়নিক সাম্যবস্থার শর্ত বা বৈশিষ্ট্যগুলো উল্লেখ কর (Mention the conditions or properties of chemical equilibrium)
উত্তরঃ
রাসায়নিক সাম্যাবস্থার উল্লেখযোগ্য বৈশিষ্ট্যগুলো হলো:
ক. উভমুখিতা (Bidirectionality): সাম্যাবস্থায় উভমুখী বিক্রিয়া উভয়দিকে গতিশীল থাকে।
খ. প্রযোজ্যতা (Applicability): সাম্যাবস্থা শুধু উভমুখী বিক্রিয়ার ক্ষেত্রে প্রযোজ্য।
গ. সংঘটন ক্ষেত্র (Field of occurrence): রাসায়নিক সাম্যাবস্থা আবদ্ধ পরিমণ্ডলে (Closed system) সৃষ্টি হয়।
ঘ. গতিবেগ (speed of movement): সাম্যাবস্থায় উভমুখী বিক্রিয়ার সম্মুখ বিক্রিয়ার গতিবেগ এবং পশ্চাৎমুখী বিক্রিয়ার গতিবেগ সমান।
ঙ. বিক্রিয়ার অসম্পূর্ণতা (Incomplete reaction): উভমুখী বিক্রিয়া একবার সাম্যাবস্থায় উপনীত হলে বিক্রিয়া কোন দিকেই সম্পূর্ণ হতে পারে না কারণ সাম্যাবস্থায় বিক্রিয়ক থেকে যে পরিমাণ উৎপাদ গঠিত হয়, ঠিক একই পরিমাণ উৎপাদ পুনরায় বিক্রিয়কে পরিণত হয়।
চ. সাম্যের অবস্থান বা উভয়দিকে সুগম্যতা (Equilibrium position or accessibility on both sides): উভমুখী বিক্রিয়া যে দিকে থেকেই শুরু করা হোক না কেন একই অবস্থানে সাম্যাবস্থা অর্জিত হবে যেমন:
\begin{array}{c} \mathrm{H}_{2}+\mathrm{I}_{2} \stackrel{450^{\circ} \mathrm{C}}{\rightleftharpoons} 2 \mathrm{HI} \\ 20 \% \quad \quad \quad \quad 80 \%\\ 2 \mathrm{HI} \stackrel{450^{\circ} \mathrm{C}}{\rightleftharpoons} \mathrm{H}_{2} + \mathrm{I}_{2} \\ 80 \% \quad \quad \quad \quad 20 \% \end{array}তুল্য পরিমাণ \mathrm{H}_{2} ও \mathrm{I}_{2} কে নিয়ে বিক্রিয়া করানো হলে বা \mathrm{HI} কে বিয়োজিত করা হলে বিক্রিয়া মিশ্রণে সর্বদাই 80% \mathrm{HI} এবং 20% \mathrm{H}_{2} ও \mathrm{I}_{2} থাকবে। অর্থাৎ, যে দিক থেকেই বিক্রিয়া শুরু করা হোক না কেন সাম্যাবস্থা একই অবস্থানে অর্জিত হবে।
ছ. নিয়ামকের প্রভাব (The effect of the regulator): রাসায়নিক সাম্যাবস্থা তাপমাত্রা, চাপ ও ঘনমাত্রা দ্বারা প্রভাবিত হয় । তবে এসব নিয়ামকের পরিবর্তন না করা হলে অর্জিত সাম্যাবস্থা অনন্তকাল ধরে চলতে থাকে।
জ. অনুঘটকে প্রভাব (Catalyst effect): অনুঘটক রাসায়নিক সাম্যাবস্থার অবস্থানের কোনো পরিবর্তন করতে পারে না। তবে অনুঘটক ব্যবহার করা হলে সাম্যাবস্থা অর্জন ধীর বা দ্রুততর হয় ।
ঝ. সাম্যের স্থায়িত্ব (Sustainability of equality): নিয়ামক (তাপ, চাপ, ঘনমাত্রা) এর কোন পরিবর্তন করা না হলে বিক্রিয়া চিরকাল একই সাম্যবস্থায় থাকবে।
প্রশ্নঃ সমসত্ত্ব ও অসমসত্ত্ব সাম্যাবস্থার বলতে কী বুঝ? (Equilibrium and homogeneity equilibrium)
উত্তরঃ
(ক) সমসত্ত্ব সাম্যাবস্থা (Equilibrium equilibrium): যে সাম্যাবস্থায় উভমুখী বিক্রিয়ার উৎপাদ ও বিক্রিয়ক একই ভৌত অবস্থায় থাকে তাকে সমসত্ত্ব সাম্যাবস্থা বলে । এ সাম্যাবস্থায় বিক্রিয়া মিশ্রণ কেবলমাত্র একই দশায় (প্রধানত গ্যাসীয় দশায়) অবস্থান করে। যেমন:
\begin{array}{l} 2 \mathrm{SO}_{2}(g)+\mathrm{O}_{2}(g) \rightleftharpoons 2 \mathrm{SO}_{3}(g) \\ \mathrm{N}_{2}(g)+3 \mathrm{H}_{2}(g) \rightleftharpoons 2 \mathrm{NH}_{3}(g) \end{array}(খ) অসমসত্ত্ব সাম্যাবস্থা (Equilibrium equilibrium): যে সাম্যাবস্থায় বিক্রিয়ক ও উৎপাদ সম্পূর্ণ ভিন্ন ভৌত অবস্থান করে তাকে অসমসত্ত্ব সাম্যাবস্থা বলে।
\mathrm{CaCO}_{3}(s) \stackrel{\Delta}{\rightleftharpoons} \mathrm{CaO}(s)+\mathrm{CO}_{2}(g)
অসমসত্ত্ব সাম্যাবস্থায় একাধিক দশা থাকে।
এছাড়া, আয়নিক সাম্যাবস্থা নামে ভিন্ন একটি সাম্যাবস্থা থাকলেও তা মূলত সমসত্ত্ব সাম্যাবস্থা। এ সাম্যাবস্থায় উৎপাদ আয়নিক অবস্থায় থাকে।
প্রশ্নঃ ভরক্রিয়ার সূত্র বা (Law of Mass Action) বিবৃত কর এবং ব্যাখ্যা কর।
উত্তরঃ
নির্দিষ্ট তাপমাত্রায় নির্দিষ্ট সময়ে যেকোনো বিক্রিয়ার হার ঐ সময়ে বিক্রিয়ায় অংশগ্রহণকারী প্রতিটি বিক্রিয়কের সক্রিয় ভরের সমানুপাতিক বা বিক্রিয়কসমূহের সক্রিয় ভরের গুণফলের সমানুপাতিক (সক্রিয় ভর বলতে মোলার ঘনমাত্রা এবং গ্যাসের ক্ষেত্রে আংশিক চাপকে বোঝানো হয় ।)
মনে করি, একটি রাসায়নিক বিক্রিয়া নিম্নরূপে সাম্যবস্থায় আছে-
A+B \rightleftharpoons C+D
ভরক্রিয়ার সূত্র মতে,
সম্মুখমূখী বিক্রিয়ার হার, R_{f} \propto[A][B]
বা, R_{f}=k_{1}[A][B]
এখানে, k_{1} হলো সম্মুখমূখী বিক্রিয়ার হার ধ্রুবক।
অনুরূপে, পশ্চাৎমূখী বিক্রিয়ার ক্ষেত্রে
R_{B} \propto[C][D]
বা, R_{B}=k_{2}[C][D]
k_{2} হলো পশ্চাৎমূখী বিক্রিয়ার হার ধ্রুবক।
সাম্যাবস্থায়, R_{f}=R_{B}.
বা, \quad k_{1}[A][B]=k_{2}[C][D]
বা, \quad \frac{k_{1}}{K_{2}}=\frac{[C] \times[D]}{[A] \times[B]}=k=k_{e q}
এই \mathrm{K} হলো সাম্যধ্রুবক বা সাম্যাঙ্ক। মোলার ঘনমাত্রার সাপেক্ষে K_{C} দ্বারা এবং আংশিক চাপের সাপেক্ষে একে K_{P} দ্বারা প্রকাশ করা হয় ।
প্রশ্নঃ সামাঙ্ক বা সাম্য ধ্রুবক বলতে কী বুঝ? (Equivalent or constant)
উত্তরঃ
স্থির তাপমাত্রায় একটি উভমূখী বিক্রিয়ায় উৎপন্ন পদার্থ সমূহের সক্রিয় ভরের গুণফল এবং বিক্রিয়ক পদার্থসমূহের সক্রিয় ভরের গুণফলের অনুপাত একটি ধ্রুবক রাশি । এই ধ্রুবক রাশিকে ঐ বিক্রিয়ার সামাঙ্ক বা সাম্য ধ্রুবক বলা হয়। উল্লেখ্য যে, বিক্রিয়ক এবং উৎপাদের সক্রিয় ভরসমূহকে যথোপযুক্ত ঘাতে উন্নীত করা হয়। এক্ষেত্রে সক্রিয় ভর বলতে মোলার ঘনমাত্রা এবং গ্যাসের ক্ষেত্রে আংশিক চাপকে বোঝানো হয়।
প্রশ্নঃ আংশিক চাপ বলতে কী বুঝ? (What is meant by partial pressure)
উত্তরঃ
নির্দিষ্ট তাপমাত্রায় পরস্পর বিক্রিয়াহীন একাধিক গ্যাস মিশ্রিত করলে মিশ্রণের মোট চাপ উপাদান গ্যাসগুলোর আংশিক চাপের সমষ্টির সমান। গ্যাস মিশ্রণের কোনো উপাদান ঐ তাপমাত্রার মিশ্রণের সম্পূর্ণ আয়তন একাকী দখল করলে যে চাপ প্রয়োগ করে, তাকে ঐ উপাদান গ্যাসের আংশিক চাপ বলে।
\text { মিশ্রণে কোনো উপাদানের আংশিক চাপ }=\frac{\text { ঐ উপাদানের মোল সংখ্যা }}{\text { মিশ্রণের মোট মোল সংখ্যা }} \times \text { মোট চাপ }
প্রশ্নঃ K_{C} বা K_{P} বলতে কী বুঝ? এদের মধ্যে সম্পর্ক নির্ণয় কর। (What is K_{C} and K_{P} and it’s relationship)
উত্তরঃ
কোনো উভমূখী বিক্রিয়ার সাম্যাবস্থায় উৎপাদসমূহের যথোপযুক্ত ঘাত বিশিষ্ট মোলার ঘনমাত্রা পদের গুণ ফল এবং বিক্রিয়ক সমূহের যথোপযুক্ত ঘাতবিশিষ্ট মোলার ঘনমাত্রা পদের গুণফল এর অনুপাত একটি ধ্রুবক রাশি। এ ধ্রুবক রাশিকে ঐ বিক্রিয়ার K_{C} বলা হয়। গ্যাসীয় সাম্যবস্থায় অবস্থানরত কোনো বিক্রিয়ার উৎপাদসমূহের যথোপযুক্ত ঘাতবিশিষ্ট আংশিক চাপের গুণফল এবং বিক্রিয়কসমূহের যথোপযুক্ত ঘাতবিশিষ্ট আংশিক চাপের গুণফলের অনুপাত সাম্যাবস্থায় বিক্রিয়াটির K_{P} বলা হয়।
মনে করি, নিম্নোক্ত বিক্রিয়াটি গ্যাসীয় সাম্যাবস্থায় আছে ।
\mathrm{aA}_{(\mathrm{g})}+\mathrm{bB}_{(\mathrm{g})} \rightleftharpoons \mathrm{lL}_{(\mathrm{g})}+\mathrm{mM}_{(\mathrm{g})}
ভরক্রিয়ার সূত্র মতে,
বিক্রিয়াটির ক্ষেত্রে, \quad K_{C}=\frac{[\mathrm{L}]^{1} \times[\mathrm{M}]^{\mathrm{m}}}{[\mathrm{A}]^{\mathrm{a}} \times[\mathrm{B}]^{\mathrm{b}}}=\frac{c_{\mathrm{L}}^{\mathrm{l}} \times c_{\mathrm{M}}^{\mathrm{m}}}{c_{\mathrm{A}}^{\mathrm{a}} \times \mathrm{c}_{\mathrm{B}}{ }^{\mathrm{b}}} \ldots \ldots \ldots (i)
অনুরূপে, \quad K_{P}=\frac{p_{L}^{\prime} \times p_{M}^{m}}{p_{A}^{a} \times p_{B}^{b}} \ldots \ldots \ldots(ii)
একটি আদর্শ গ্যাস মিশ্রণে কোনো একটি উপাদান গ্যাসের n মোলের আংশিক চাপ P হলে এবং ঐ গ্রাসটি T তাপমাত্রায় V লিটার আয়তন দখল করলে, আদর্শ গ্যাস সমীকরণ মতে,
\mathrm{PV}=\mathrm{nRT}
বা, P=\frac{n}{V} \cdot R T
বা, P= CRT \left[C=\frac{n}{V}\right]
এই মান \mathrm{K_{P}} এর সমীকরণে বাসয়ে পাই,
বা, \mathrm{K}_{\mathrm{P}}=\frac{\left(C_{L} R T\right)^{I} \times\left(C_{M} R T\right)^{m}}{\left(C_{A} R T\right)^{a} \times\left(C_{B} R T\right)^{b}}
\begin{array}{l} =\frac{C_{L}^{l} \times C_{M}^{m}}{C_{A}^{a} \times \mathrm{C}_{\mathrm{B}}^{\mathrm{b}}} \times \frac{(R T)^{l+m}}{(R T)^{a+b}} \\ =K_{C} \times(R T)^{(l+m)-(a+b)}\\ =K_{C}(R T)^{\Delta n} \end{array}
\Delta n= উৎপাদের এবং বিক্রিয়কের মোল সংখ্যার পরিবর্তন]
এটি হলো \mathrm{K_{C}} এবং \mathrm{K_{P}} এর মধ্যে নির্ণেয় সম্পর্ক।
যে সমস্ত বিক্রিয়ার ক্ষেত্রে, \Delta n=0,\left(H_{2}+I_{2} \rightleftharpoons 2 H I\right)
সেক্ষেত্রে, \begin{array}{c} K_{P}=K_{C} \times(R T)^{0} \\ \therefore K_{P}=K_{C} \end{array}
প্রশ্নঃ সাম্যধ্রুবকের তাৎপর্য উল্লেখ কর। (Significance of Equilibrium)
উত্তরঃ
- নির্দিষ্ট তাপমাত্রায় কোনো বিক্রিয়ার সাম্যধ্রুবকের মান নির্দিষ্ট কোন বিক্রিয়া একবার সাম্যবস্থার পৌছালে নিয়ামকসমূহ পরিবর্তন করা হলে সাম্যবস্থা এমনভাবে পরিবর্তিত হয় যেন সাম্যধ্রুবক এর মান স্থির থাকে।
- সাম্যধ্রুবকের মান হতে কোনো বিক্রিয়া প্রদত্ত কতটুকু সম্পন্ন হবে তা বোঝা যায়। যেমন- K_{C}, K_{P} এর মান তুলনামূলকভাবে বেশি হলে তা অধিকতর উৎপাদের জন্য অনুকূল বুঝায়। অপরদিকে মান কম হলে তা অধিক উৎপাদের জন্য অনুকূল নয় বোঝায়।
প্রশ্নঃ সামধ্রুবকের মান কখনও শূণ্য বা অসীম হতে পারে না কেন? \boldsymbol{K_{C}} এর মান কখনও শূণ্য বা অসীম হয় না কেন? (Why the value of equilibrium can never be zero or infinite?) (Why is the value of \boldsymbol{K_{C}} never zero or infinite?)
উত্তরঃ
কোনো উভমূখী বিক্রিয়া সাম্যবস্থায় উপনীত হলে সম্মুখমূখী এবং পশ্চাৎমুখী বিক্রিয়া একই হারে চলতে থাকে তাই সাম্যধ্রুবকের মান শূণ্য বা অসীম হতে পারে না । মনে করি, একটি বিক্রিয়া নিম্নরূপে সম্পন্ন হয়েছে-
A \rightleftharpoons B
এই বিক্রিয়াটির ক্ষেত্রে,K_{C}=\frac{[B]}{[A]} \ldots \ldots \ldots \ldots(i)
যদি K_{C}=0 হয় তবে (i) নং সমীকরণের [B]=0 হতে হবে। অর্থাৎ, K_{C}=\frac{0}{[A]}=0
কিন্তু সাম্যবস্থায় অবস্থানরত কোনো উভমূখী বিক্রিয়া উৎপাদের ঘনমাত্রা কখনও শূণ্য হতে পারে না। কারণ বিক্রিয়া কখনও উৎপাদ শূন্য হয়। তাই, K_{C} \neq 0.
আবার, K_{C}=\propto হলে (i) নং সমীকরণের [A] = 0 হতো অর্থাৎ, K_{C}=\frac{[B]}{0}=\propto
কিন্তু সাম্যবস্থায় বিক্রিয়কের ঘনমাত্রা কখনও শূণ্য হতে পারে না। তাই K_{C} \neq \propto অর্থাৎ, কেবলমাত্র একমূখী বিক্রিয়ার ক্ষেত্রে K_{C} মান শূন্য বা অসীম হবে কিন্তু উভমুখী বিক্রিয়া ক্ষেত্রে নয়।
প্রশ্নঃ K_{C} এবং K_{P} এর একক নির্ণয় কর। (Unit of K_{C} and K_{P})
উত্তরঃ
১। যে সমস্ত বিক্রিয়ার ক্ষেত্রে \Delta n=0 সেহেতু, K_{C} এবং K_{P} এককবিহীন হবে।
২। যে সমস্ত বিক্রিয়ায় \Delta n=1 হলে, সেক্ষেত্রে K_{C} এর একক \operatorname{molL}^{-1} এবং K_{P} এর একক atm বা pa বা \mathrm{Nm}^{-2} একক হবে।
\begin{array}{c} A \rightleftharpoons 2 B \\ K_{c}=\frac{[B]^{2}}{[A]}=\frac{m p l^{2} L^{-2}}{m o l L^{-1}}=m o l L^{-1} \end{array}সাম্যধ্রুবকের কোন একক নেই কারণ সক্রিয়ভরের কোনো একক থাকে না । তবে কোনো কোনো ক্ষেত্রে একক আকারে প্রকাশ করা হয়।
৩। \Delta n=-1 হলে, সেক্ষেত্রে K_{C} এর একক হবে \mathrm{Lmol}^{-1} এবং K_{P} এর একক হবে \mathrm{atm}^{-1}
2 A \rightleftharpoons B
এই বিক্রিয়ার K_{p}=\frac{P_{B}}{P_{A}^{2}}=\frac{\mathrm{atm}}{\mathrm{atm}^{2}}=\mathrm{atm}^{-1}
\Delta n=2-4=-2
K_{C} এর একক \quad L^{2} \mathrm{~mol}^{-2}
K_{P} এর একক হবে (\mathrm{atm})^{-2}
প্রশ্নঃ বিয়োজনের পরিমাণ এবং বিয়োজন মাত্রা বলতে কী বুঝ? (What is meant by the amount of subtraction and the degree of subtraction)
উত্তরঃ
বিয়োজনের পরিমাণ বলতে বিক্রিয়কের যত মোল বিয়োজিত হয়ে উৎপাদে পরিণত হয়েছে সে পরিমাণকে বোঝায়। যেমন- 5 মোল পদার্থের 2 মোল বিয়োজিত হলে তাহলে বিয়োজনের পরিমাণ হবে 2। অপরদিকে, বিয়োজনের মাত্রা বলতে কোনো পদার্থের বা উপাদানের মোল সংখ্যার কত ভগ্নাংশ বিয়োজিত হয়েছে সে সংখ্যাকে বোঝায়।
বিয়োজন মাত্রাকে তথা এই ভগ্নাংশকে অনেক ক্ষেত্রে শতকরা হিসাবে প্রকাশ করা হয়। যেমন- কোনো বিক্রিয়কের প্রাথমিক অবস্থায় 5 মোল বিক্রিয়ক নিয়ে বিক্রিয়া শুরু করলে এর 2 মোল বিয়োজিত হলে তখন বিয়োজনের পরিমাণ হবে 2 এবং বিয়োজন মাত্রা হচ্ছে \frac{2}{5} বা 0.4 বা 40%
প্রশ্নঃ নিম্নোক্ত বিক্রিয়ার K_{C} এবং K_{P} এর রাশিমালা নির্ণয় কর। (Expression of K_{C} and K_{P})
উত্তরঃ
H_{2}(g)+I_{2}(g) \rightleftharpoons 2 H I(g)
মনে করি, v লিটার আয়তনবিশিষ্ট একটি আবদ্ধ পাত্রে a mol \mathrm{H}_{2} এবং b mol \mathrm{I}_{2} নিয়ে একটি নির্দিষ্ট তাপমাত্রায় উত্তপ্ত করে বিক্রিয়াটি শুরু করা হল। দেখা গেল যে, সাম্যবস্থায় \alpha মোল \mathrm{HI} উৎপন্ন হল।
∴ সাম্যাবস্থায় K_{C} এবং K_{P} এর মোলসংখ্যা যথাক্রমে (a-\alpha) এবং (b-\alpha) করে হবে। বিষয়টিকে নিমোরূপে দেখানো যায়।
\begin{array}{lccc} \text { মনে করি } & \mathrm{H}_{2}(g)+ & l_{2}(g) & \rightleftharpoons 2 \mathrm{HI} \\ \text { ১ম অবস্থায় : } & 1 \mathrm{~mol} & 1 \mathrm{~mol} & 0 \mathrm{~mol} \\ \text { সাম্যবস্থ|য় : } & (a-\alpha) & (b-\alpha) & 2 \alpha \mathrm{mol} \\ & \mathrm{mol} & \mathrm{mol} & \end{array}
K_{C} নির্ণয়:
সাম্যবস্থায় \mathrm{H}_{2} এর মোলার ঘনমাত্রা \left[\mathrm{H}_{2}\right] বা \mathrm{C}_{H_{2}}
=\frac{a-\alpha}{v} \operatorname{mol} L^{-1}সাম্যবস্থায় I_{2} এর মোলার ঘনমাত্রা \left[I_{2}\right] বা C_{l_{2}}=\frac{b-\alpha}{v} \operatorname{mol} L^{-1}
সাম্যবস্থায় HI এর মোলার ঘনমাত্রা [H I] বা C_{H I}=\frac{2 \alpha}{v} \operatorname{molL}^{-1}
\therefore \quad K_{C}=\frac{[\mathrm{Hl}]^{2}}{\left[\mathrm{H}_{2}\right]\left[l_{2}\right]} \frac{C_{H I}^{2}}{C_{H_{2}} \times C_{I_{2}}}\therefore বিক্রিয়াটির K_{C}=\frac{[H l]^{2}}{\left[H_{2}\right]\left[l_{2}\right]} \frac{C_{H I}^{2}}{C_{H_{2}} \times C_{I_{2}}}
=\frac{\left(\frac{2 \alpha}{\mathrm{V}}\right)^{2}}{\frac{\mathrm{a}-\alpha}{\mathrm{V}} \cdot \frac{\mathrm{b}-\alpha}{\mathrm{V}}}=\frac{4 \propto^{2}}{(\mathrm{a}-\alpha)(\mathrm{b}-\alpha)}যেহেতু \Delta n=0 সেহেতু এককবিহীন।
K_{P} নির্ণয়:
এ বিক্রিয়ার ক্ষেত্রে \Delta n=2-2=0
সুতরাং,
\begin{aligned} K_{P} &=K_{C} \times(R T)^{\Delta n} \\ K_{P} &=K_{C} \end{aligned} \therefore K_{P}=\frac{4 \alpha^{2}}{(a-\alpha)(b-\alpha)}
প্রশ্নঃ N_{2} O_{4} বিযোজন বিক্রিয়ার K_{c} এবং K_{P} নির্ণয় কর।
প্রদত্ত বিক্রিয়া \mathrm{N}_{2} \mathrm{O}_{4} \rightleftharpoons \quad 2 \mathrm{NO}_{2}
প্রাথমিক অবস্থা 1 \mathrm{~mol} \quad 0 \mathrm{~mol}
সাম্যবস্থায় \quad(1-\propto) \mathrm{mol} \quad 2 \propto \mathrm{mol}
\mathrm{N}_{2} \mathrm{O}_{4} এর মোলার ঘনমাত্রা, \left[\mathrm{N}_{2} \mathrm{O}_{4}\right]=\frac{1-\propto}{v} \operatorname{mol} \mathrm{L}^{-1}
\mathrm{NO}_{2} এর মোলার ঘনমাত্রা, \left[\mathrm{NO}_{2}\right]=\frac{2 \propto}{v} \mathrm{molL}^{-1}
মনে করি, v আয়তনবিশিষ্ট আবদ্ধ পাত্রে বিক্রিয়াটি সম্পন্ন হয়।
\begin{aligned} \therefore \quad K_{C} &=\frac{\left[N O_{2}\right]^{2}}{\left[N_{2} O_{4}\right]} \\ &=\frac{\frac{\left(\frac{2 \alpha}{v}\right)^{2}}{1-\alpha}}{v} \\ &=\frac{4 \alpha^{2}}{v^{2}} \times \frac{v}{1-\alpha}=\frac{4 \alpha^{2}}{v(1-\alpha)} \operatorname{molL}^{-1} \end{aligned}K_{P} নির্ণয়:
মনে করি, মিশ্রনের মোট চাপ =P \mathrm{~atm}
মোট মোলসংখ্যা =1-\alpha+2 \propto=1+\alpha
\mathrm{N}_{2} \mathrm{O}_{4} এর আংশিক চাপ P_{\mathrm{N}_{2} \mathrm{O}_{4}}=\frac{1-\propto}{1+\alpha} . Patm
\mathrm{NO}_{2} এর আংশিক চাপ \mathrm{P}_{\mathrm{NO}_{2}}=\frac{2 \propto}{1+\alpha} . Patm
=\frac{2 \propto P}{1+\alpha} . \text { atm }
\begin{aligned}
\therefore \mathrm{K}_{\mathrm{p}} &=\frac{\left(P_{\mathrm{NO}_{2}}\right)^{2}}{P_{N_{2} O_{4}}}=\frac{\left(\frac{2 \propto P}{1+\alpha}\right)^{2}}{\frac{P(1-\alpha)}{1+\alpha}} \\
&=\frac{4 \propto^{2} P^{2}}{(1+\propto)^{2}} \cdot \frac{(1+\alpha)}{P(1-\propto)}=\frac{4 \alpha^{2} \times P}{\left(1-\alpha^{2}\right)} \mathrm{atm}
\end{aligned}
এ বিক্রিয়ার ক্ষেত্র বিয়োজনের পরিমাণ \propto ধ্রুবই ক্ষুদ্র হুলে 1-\alpha \approx 1
অর্থাৎ, বিক্রিয়াটির ক্ষেত্রে চাপ এবং বিয়োজনের পরিমাণ পরস্পরের ব্যাস্তানুপাতিক। অর্থাৎ, চাপ বৃদ্ধি করলে \mathrm{N}_{2} \mathrm{O}_{4} এর বিয়োজনের পরিমাণ হ্রাস পায় এবং চাপ হ্রাস করলে \mathrm{NO}_{2} এর বিয়োজনের পরিমাণ হ্রাস পায়।
