গতি বিষয়ক লেখচিত্র

পদার্থবিজ্ঞানে সময়ের সাথে কোন বস্তুর সরণের হারকে গতি/বেগ (motion)  বলে। সময়ের সাপেক্ষে আমরা গতি বিষয়ক বিভিন্ন লেখচিত্র ও এর ব্যাখা দেখব।

গতি বিষয়ক লেখচিত্র (Motion Related Graphs)

অবস্থান-সময় লেখচিত্র (Position-time Graph)

১. কোনো বস্তু একটি নির্দিষ্ট বিন্দু থেকে কোনো নির্দিষ্ট দূরত্বে অবস্থিত হলে সেই বিন্দু থেকে বস্তুর দূরত্বকে অবস্থান
  (position) বলে।

মনে কর, একটি বস্তু X-অক্ষ বরাবর গতিশীল। বস্তুটি P বিন্দুতে তখন মূলবিন্দু O থেকে বস্তুটির দূরত্ব x1 এবং Q বিন্দুতে যখন অবস্থান করে তখন দূরত্ব x2। X-অক্ষ বরাবর বস্তুর এরূপ গতি চিত্র দ্বারা প্রকাশ করা যায়।

   

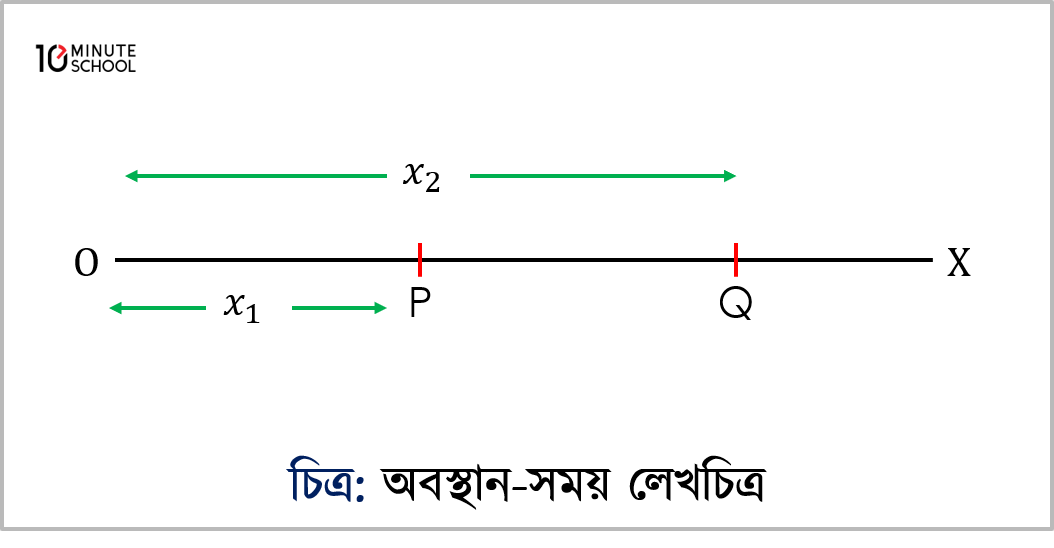
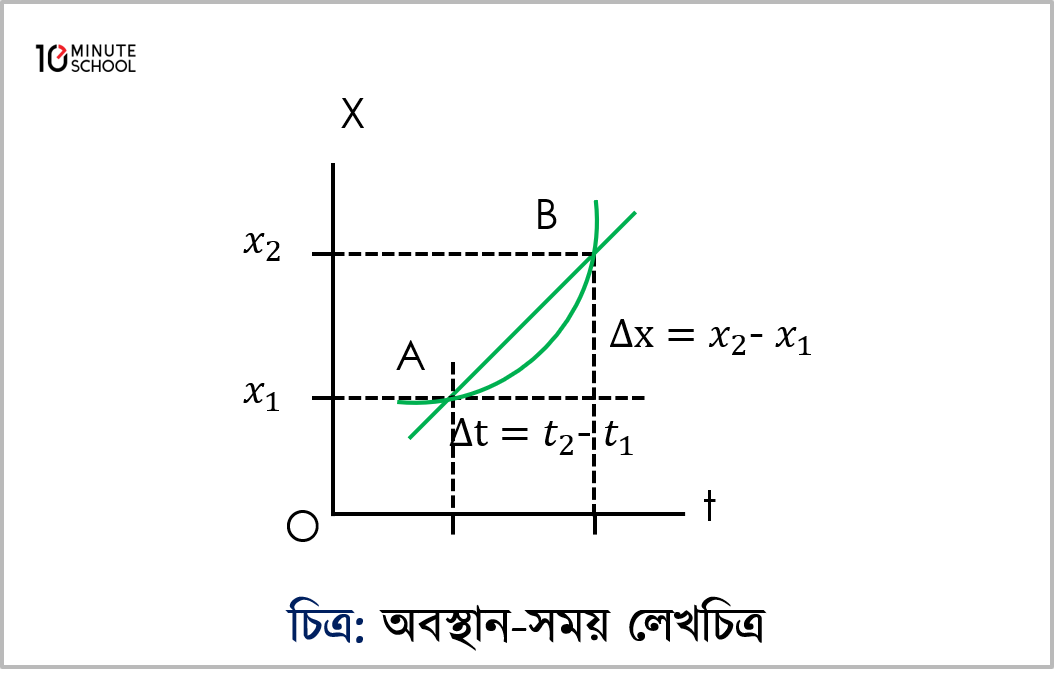
আবার, মনে করি, কোনো একটি বস্তু t1 সময়ে A বিন্দুতে এবং t2 সময়ে B বিন্দুতে অবস্থান করে । X-অক্ষ বরাবর A ও B বিন্দুর স্থানাঙ্ক যথাক্রমে x1 এবং x2এক্ষেত্রে t2 এবং t1সময়ের মধ্যকার ব্যবধান ∆t = t2 –t1  চিত্র এ দেখানো হলো।

দূরত্ব সময় লেখচিত্র (Distance-time Graphs)

(i) দূরত্ব-সময় লেখচিত্র (সমবেগের ক্ষেত্রে):

একটি মোটর সাইকেলের গতি সমতল রাস্তায় ২ মিনিট পরপর নিচের সারণিতে দেখান হলো।

সময় t(min)	দূরত্ব s(km)
0	0
2	4
4	8
6	12

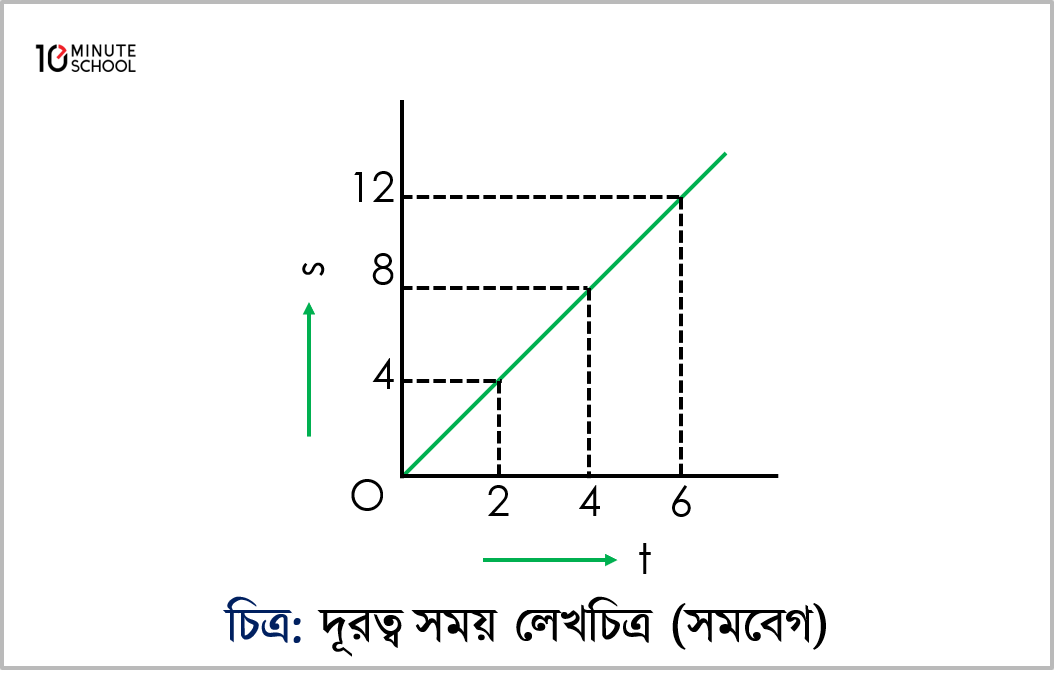
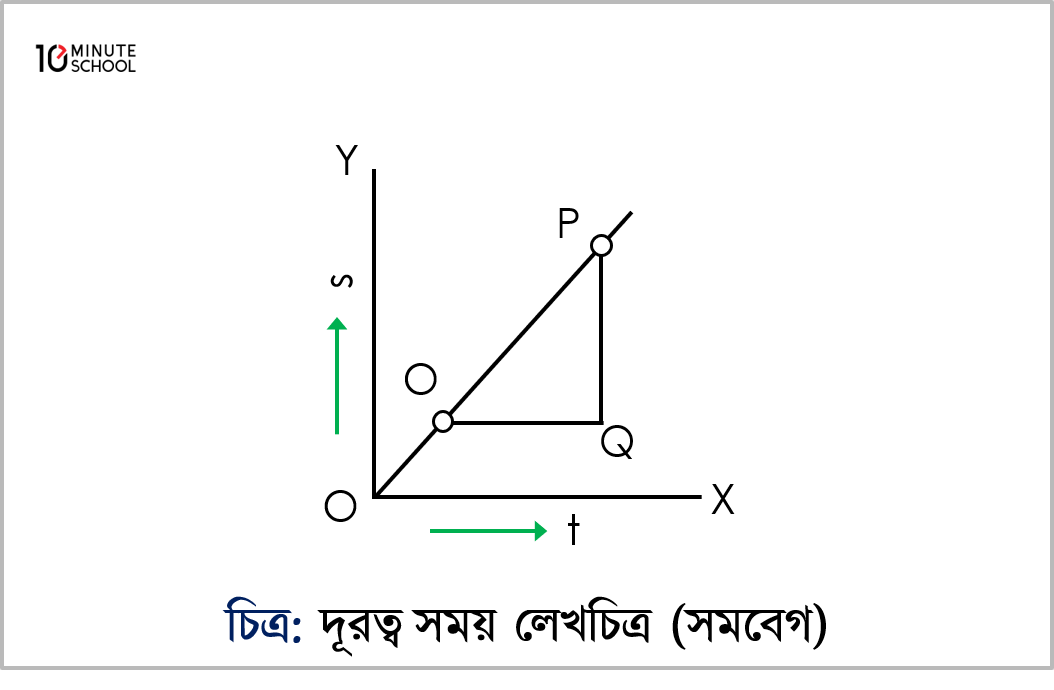
সমবেগে গতিশীল বস্তু একই সময়ে একই দূরত্ব অতিক্রম করবে। সুতরাং সময় সাপেক্ষে দূরত্বের লেখচিত্র মূল বিন্দুগামী একটি সরলরেখা OP হয়।

OP রেখার ঢাল =PQOQ=দুরত্বসময়= বেগ

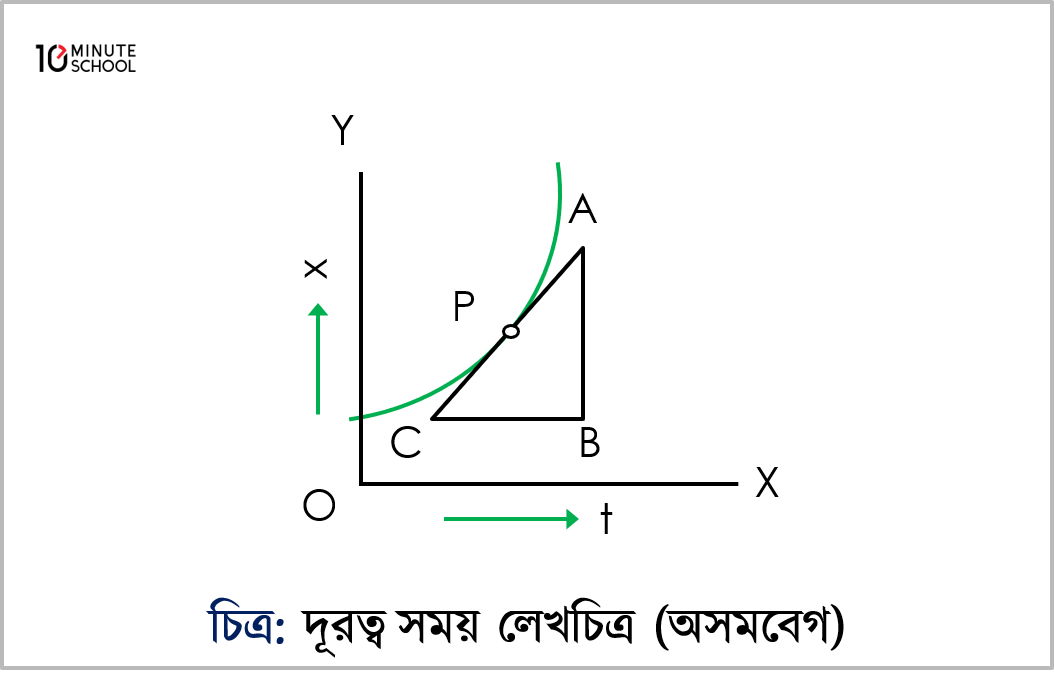
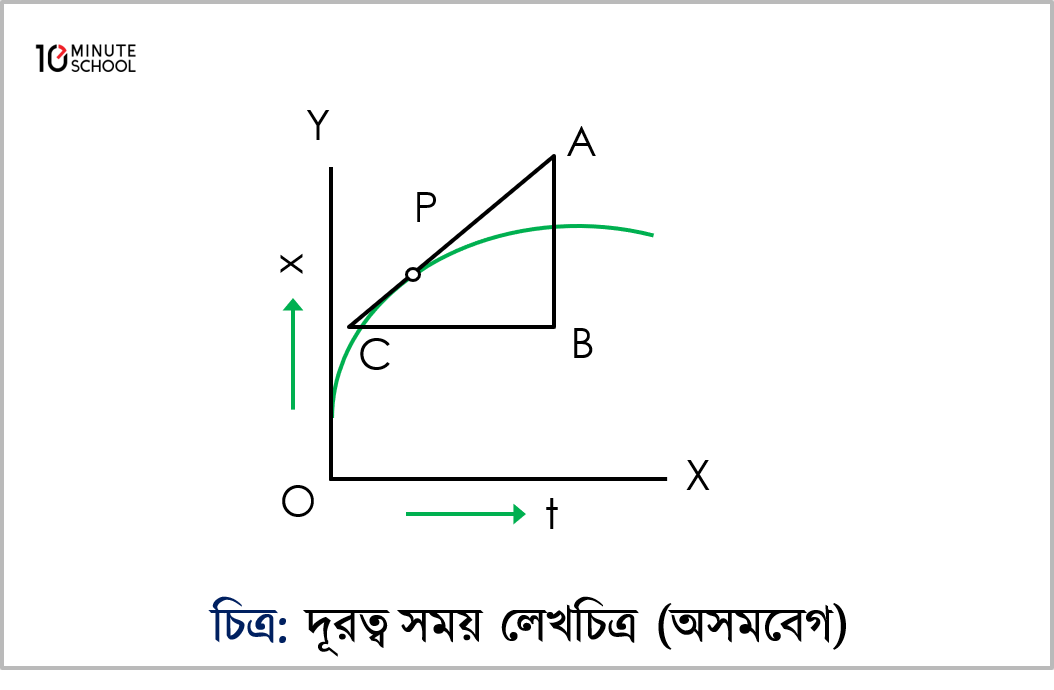
(ii) দূরত্ব-সময় লেখচিত্র (অসম বেগের ক্ষেত্রে):

অসম বেগে গতিশীল বস্তু একই সময়ে একই দূরত্ব অতিক্রম করে না। অবস্থান (x) ও সময় (t) এর লেখচিত্র বক্ররেখা হয়। যেকোন সময় বেগ নির্ণয়ে ঐ বিন্দু হতে স্পর্শক টেনে ঢাল নিলে বেগ পাওয়া যায়। চিত্রে P বিন্দুতে বেগ নির্ণয় করা হয়েছে।

অতএব বস্তুর সমবেগ দূরত্ব-সময় লেখচিত্রের নতির সমান হয়। অর্থাৎ যে কোন সময়ে বেগের মান হবে ঐ বিন্দুতে অঙ্কিত ঢালের মান।

এরূপ বক্ররেখার ঢাল বিভিন্ন বিন্দুতে বা ভিন্ন ভিন্ন সময়ে ভিন্ন হয়। এই ঢালের মান ঐ সময়ে অসম বেগের মান নির্দেশ করে।

চিত্র অনুযায়ী, P বিন্দুতে বেগ =ABCB 

বেগ-সময় লেখচিত্র (Velocity-time Graphs)

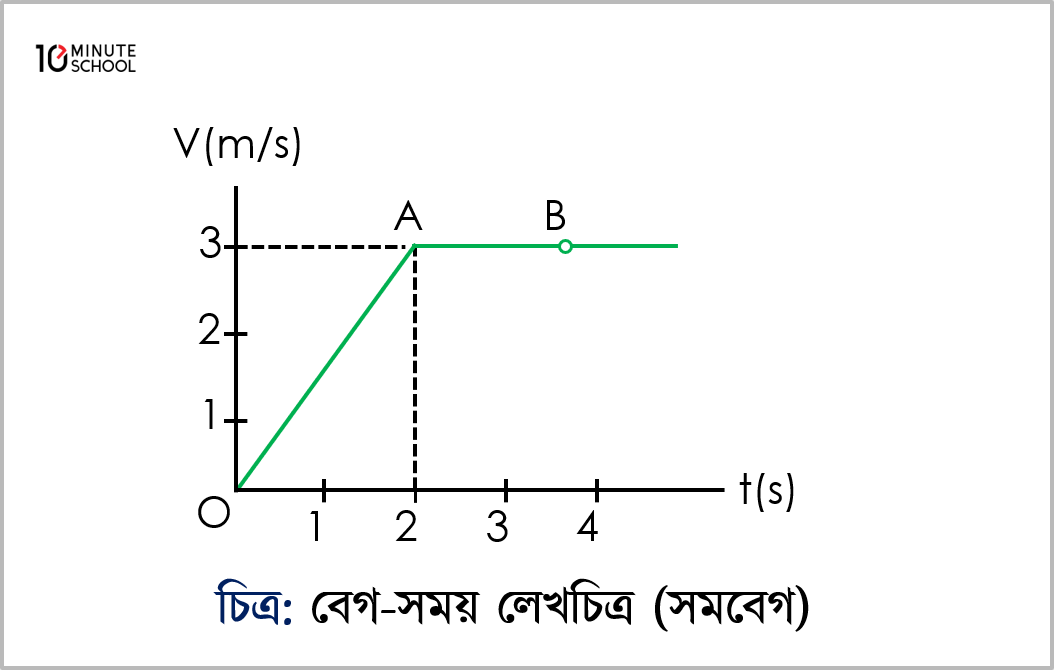
(i) বেগ সময় লেখচিত্র (সমবেগের ক্ষেত্রে):

    

সমবেগে চলমান বস্তুর সময় সাপেক্ষে বেগের লেখচিত্র সময় অক্ষেরসমান্তরাল সরলরেখা CB হয় [চিত্র]। সময়ের সাথে বেগের কোন পরিবর্তন হয় না বলেই এরকম হয়।

বেগ-সময় লেখচিত্রে বেগ ও সময় অক্ষ দ্বারা সীমাবদ্ধ OABC আয়তক্ষেত্রের ক্ষেত্রফল =OC×OA=vt=s 

   

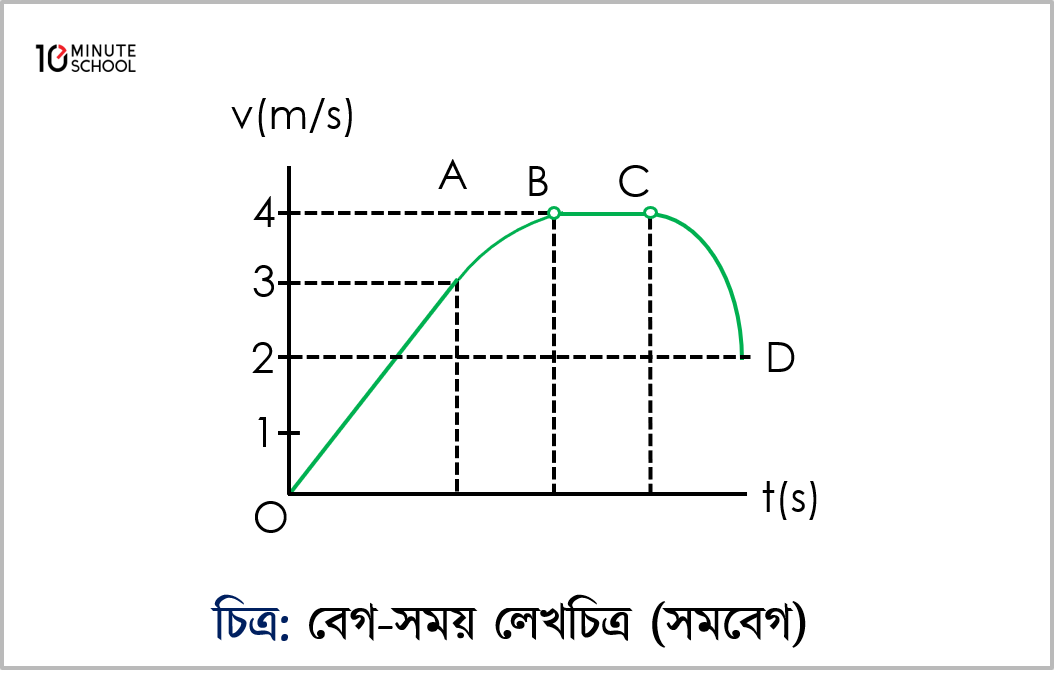
(ii) বেগ-সময় লেখচিত্র (অসমবেগের ক্ষেত্রে):

t=0sec  থেকে 2sec পর পর বেগ হ্রাসের মান সারণি দেওয়া হলো। প্রাপ্ত মান থেকে v-t লেখচিত্র অঙ্কন করলে লেখচিত্রটি নিম্নরূপ হয় (চিত্র)।

 

সময় t(sec)	বেগ v(ms-1)
0	14
2	12
4	10
6	8
8	6
10	4
12	0

এই লেখচিত্রে যে কোন সময় t-তে বস্তুর বেগ v যা নির্ণয় করা যায়। চিত্র থেকে দেখা যায় সময়ের সাথে সাথে বেগ হ্রাস পায়। চিত্র থেকে আরও দেখা যায়, 0 সময়ে বস্তুর বেগ 14 ms-1 এবং 12 sec⁡ সময়ে বেগ শূন্য। এটি একটি অসম বেগ। এক্ষেত্রে সময়ের সাথে সাথে বেগ হ্রাস পাচ্ছে এবং প্রতিক্ষেত্রে ত্বরণ (বা মন্দন) ধ্রুব থাকে।

(iii) বেগ-সময় লেখচিত্র (সমত্বরণের ক্ষেত্রে): 

সমত্বরণে সরলরেখা বরাবর সচল বস্তুর বেগ-সময়লেখচিত্রটি একটি সরলরেখা হয়। একই সময় অবকাশে একই পরিমাণ বেগ বৃদ্ধি হয় বলে লেখচিত্রটি এরূপ হয়। বস্তুটি স্থির অবস্থান থেকে যাত্রা শুরু করলে সরলরেখাটি, মূল বিন্দুগামী হয়, (ক) চিত্রে OB সরলরেখা। এই সরলরেখার ঢাল থেকে ত্বরণ নির্ণয় করা যায়।

     

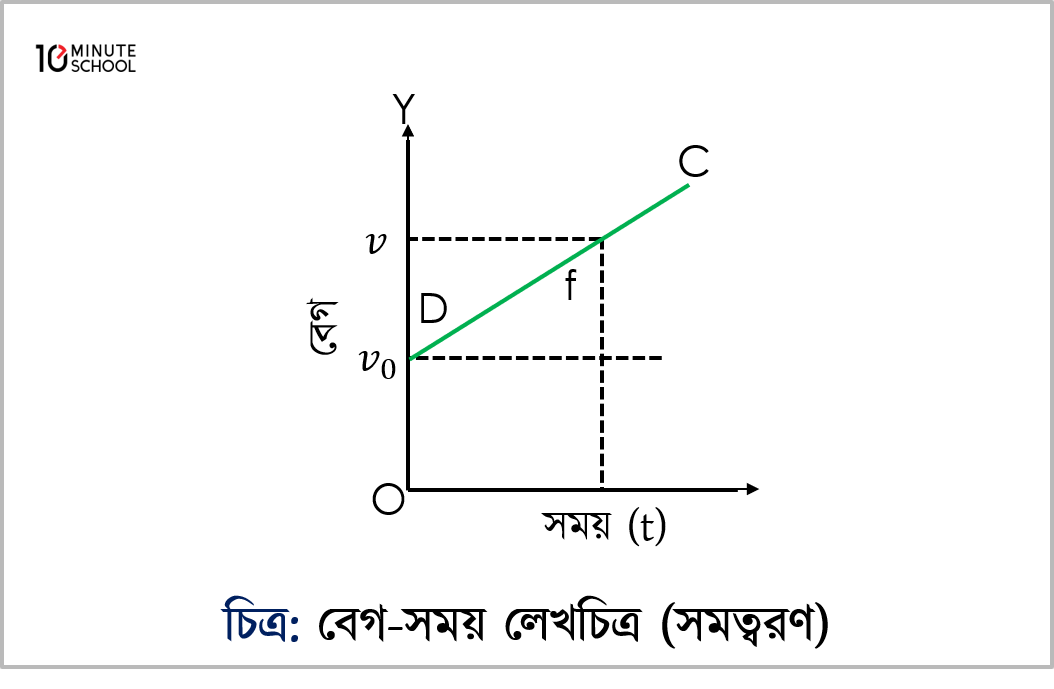
কিন্তু বস্তুটির প্রাথমিক বেগ থাকলে বেগ-সময় লেখচিত্রটি DC সরলরেখা হয় [চিত্র ৩.২৫(খ)]। এখানে OD = প্রাথমিক বেগ v0। দুটি ক্ষেত্রেই সরলরেখাটির নতি বা ঢাল বস্তুর সমত্বরণের সমান হয়।

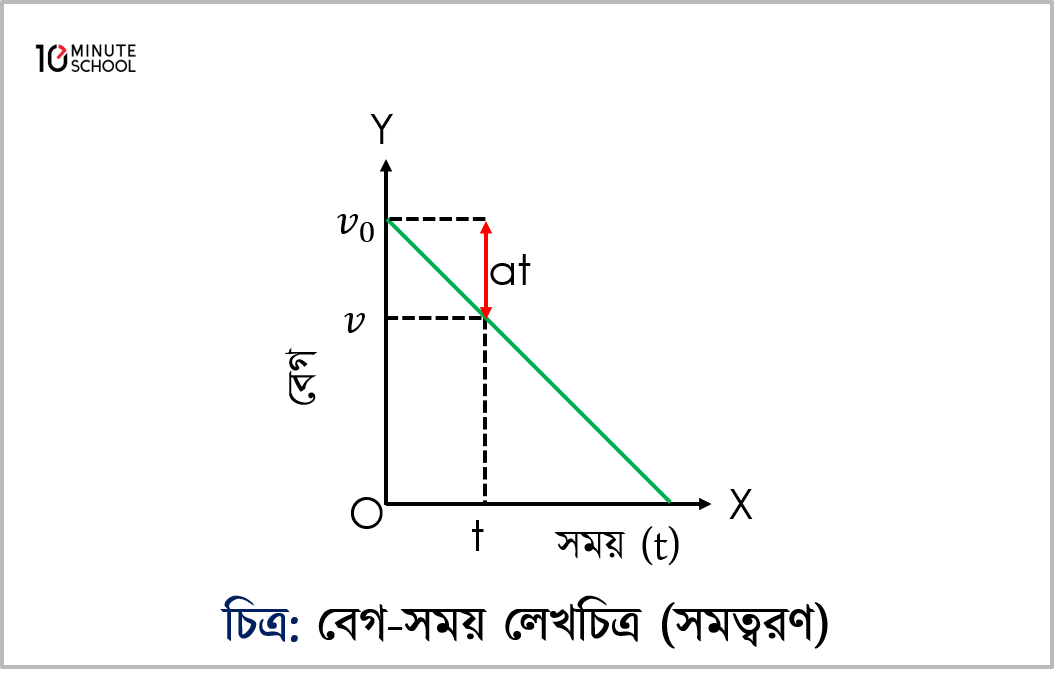
(iv) বেগ-সময় লেখচিত্র (সম-মন্দনের ক্ষেত্রে): সম মন্দনে চলমান বস্তুর প্রাথমিক বেগ থাকবেই। এক্ষেত্রেও বেগ–সময় লেখচিত্রটি সরলরেখা হবে। কিন্তু এর ঢাল ঋণাত্মক হবে [চিত্র ৩.৩১(গ)]। ঋণাত্মক ঢাল মন্দন বুঝায়। সরলরেখাটির ঢাল বস্তুর সম মন্দনের সমান হয়। শেষ পর্যন্ত বস্তুটি স্থির অবস্থায় আসে অর্থাৎ এর বেগ শূন্য হয়।

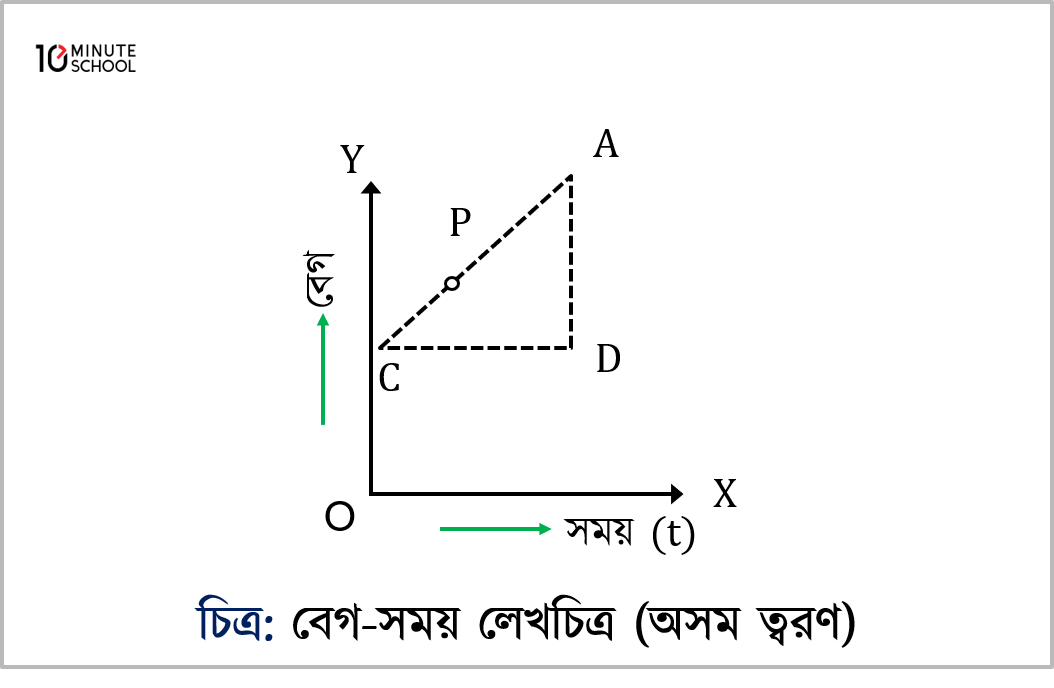
(v) বেগ-সময় লেখচিত্র (অসম ত্বরণের ক্ষেত্রে): অসম ত্বরণে চলমান বস্তুর ক্ষেত্রে বেগ–সময় লেখচিত্রটি বক্ররেখা হয় [চিত্র (ক) ও (খ)]। সময়ের সঙ্গে বেগ বাড়লে ত্বরণও বাড়ে লেখচিত্র ৩.৩২(ক), (খ)-এর অনুরূপ হয়। পূর্বের মতো আমরা প্রমাণ করতে পারি যে, (t1–t2) সময় অবকাশে গড় ত্বরণের মান AB জ্যা-এর ঢালের সমান হয়। লেখচিত্রের যেকোন বিন্দুতে তাৎক্ষণিক ত্বরণ ঐ বিন্দুতে লেখচিত্রের স্পর্শকের ঢালের সমান হয়। সময়ের সঙ্গে লেখচিত্রটির ঢাল বাড়তে থাকে। এ থেকে বোঝা যায় যে, ত্বরণ স্থির নয় [চিত্র ৩.২৬(খ)] বরং সময়ের সঙ্গে বাড়ছে। 

  

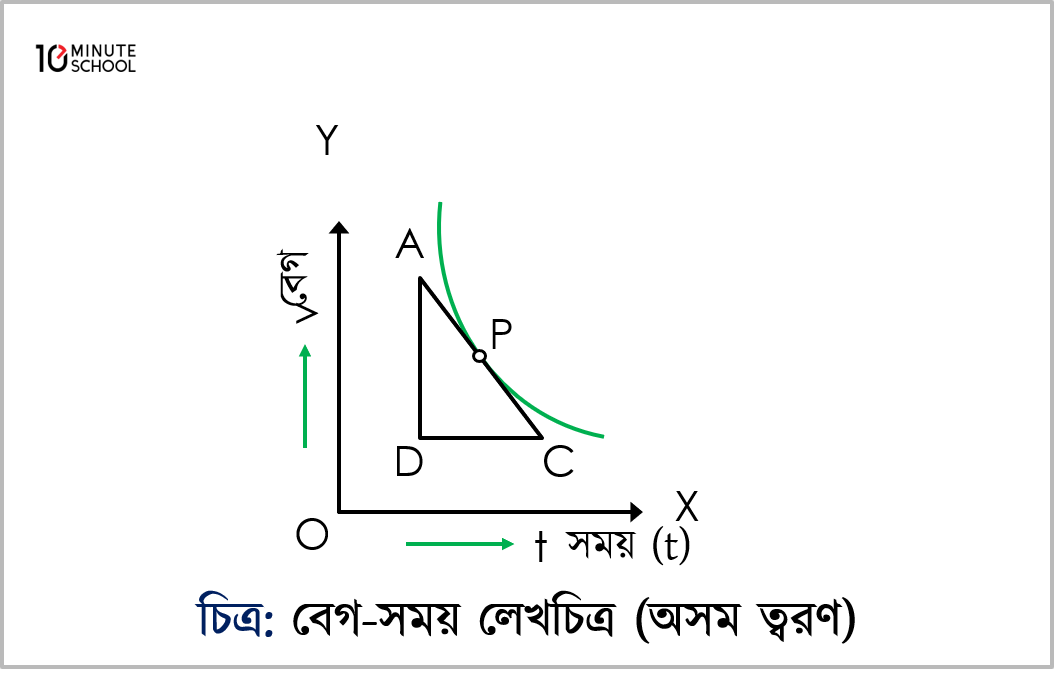
বস্তুর বেগ সময়ের সাথে কমলে বা মন্দন হলে লেখচিত্রটি ৩.৩২(গ) চিত্রের অনুরূপ হয়। P বিন্দুর ত্বরণ AADC এর ঢাল থেকে পাওয়া যায়।

∴ ত্বরণ = ঢাল = ADDC

(a) v=v0+at  সমীকরণের ক্ষেত্রে লেখচিত্র

এই সমীকরণে দুটি চলরাশি আছে, একটি হলো সময় t অপরটি হলো বেগ v। t কে X অক্ষে এবং কে Y অক্ষে স্থাপন করে একটি বস্তুকণার বেগ-সময় লেখচিত্র আঁকা হলো [চিত্র]। চিত্রে P বিন্দু হতে Y অক্ষের উপর PY লম্ব টানি। মনে করি t সময়ে বস্তুর চূড়ান্ত বেগ =v=OY; এখন OY=OA+AY  অর্থাৎ v=v0+at. 

  

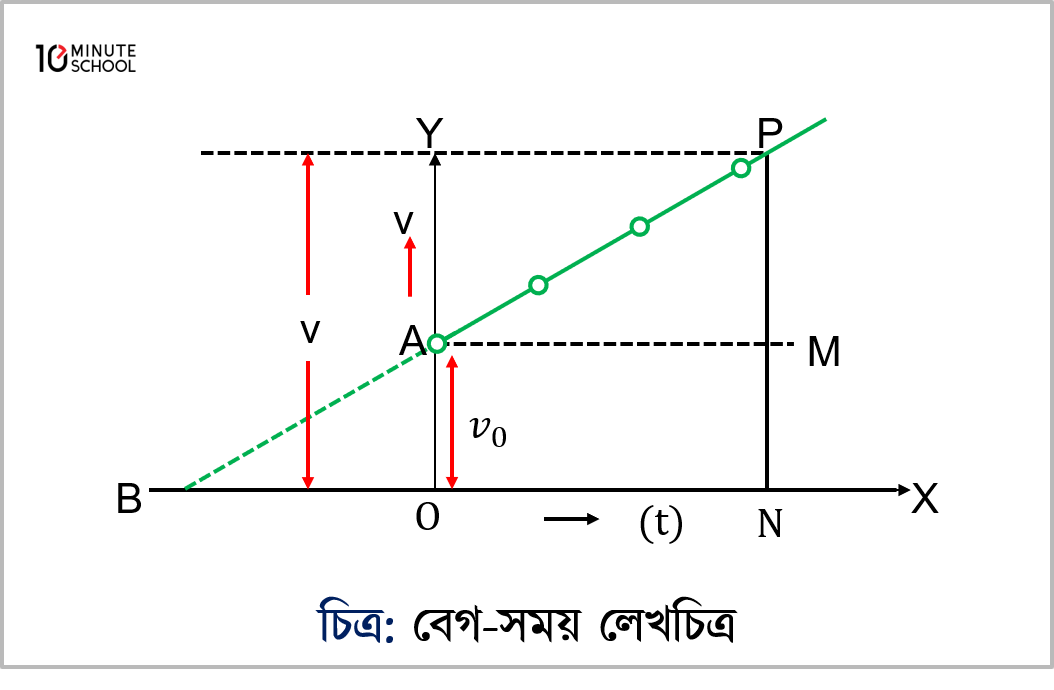
এখানে ঢাল, a=PMAM=AYAM=AYt

∴v=v0+at সমীকরণটি লেখচিত্রে উপস্থাপন করা যায়।

স্থির অবস্থান থেকে চলমান বস্তুর ক্ষেত্রে v0=0,  a= ধ্রুবক হয় ∴ v= 0+ ধ্রুবক × t   ∴v∝t

অর্থাৎ বেগ সময়ের সমানুপাতিক।

b s=v0t+12at2 সমীকরণের ক্ষেত্রে লেখচিত্র

চিত্রে v বনাম t লেখচিত্রটি একটি সরলরেখা। চিত্রে PN⊥OX;AM⊥PN

ধরি, আদি বেগ =v0 , সমত্বরণ =a, ON=t  এবং t সময়ে অতিক্রান্ত দূরত্ব =s.

এখন, s = OAPN ক্ষেত্রের ক্ষেত্রফল

             = QAMN আয়তক্ষেত্রের ক্ষেত্রফল + AMP ত্রিভুজের ক্ষেত্রফল।

             =OA×ON+12×AM×PM=v0t+12×AM×PM

আবার ঢাল, a=PMAM=PMt

∴PM=at

∴s=v0t+12t×at=v0t+12at2

স্থির অবস্থান থেকে সমত্বরণে চলমান বস্তুর ক্ষেত্রে s=0×t+12 ধ্রুবক t2

বা, s= ধ্রুবক t2

বা, s∝t2

অর্থাৎ সরণ সময়ের বর্গের সমানুপাতিক।

অনুরূপভাবে রেগ-সময় লেখচিত্রের সাহায্যে v2=v02+2as  প্রতিপাদন করা যায়। এক্ষেত্রে স্থির অবস্থান এবং সমত্বরণে চলমান বস্তুর ক্ষেত্রে v∝s হয়। অর্থাৎ বেগ দূরত্বের বর্গমূলের সমানুপাতিক।