γ-এর মানের ভিন্নতা ও গুরুত্ব | Importance and Difference of gamma/specific heat

γ- এর মানের ভিন্নতা (Variation in the values of gamma/specific heat):

আমরা জানি, \gamma = \frac{C_P}{C_V}=\frac{স্থির চাপে গ্যাসের আপেক্ষিক তাপ}{স্থির আয়তনে গ্যাসের আপেক্ষিক তাপ}

এক পারমাণবিক গ্যাসের ক্ষেত্রে (Specific Heat for Monatomic Gas)

C_V=\frac{3}{2}R এবং

C_P=C_V+R=\frac{3}{2}R+R=\frac{5}{2}R

\gamma = \frac{C_P}{C_V}=\frac{\frac{5}{2}R}{\frac{3}{2}R}=1.67, অর্থাৎ এক পারমাণবিক গ্যাসের ক্ষেত্র \gamma=1.67

দ্বিপারমাণবিক গ্যাসের ক্ষেত্রে (Specific Heat for Diatomic Gas)

C_V=\frac{5}{2}rR এবং

C_P=C_V+R=\frac{5}{2}R+R=\frac{7}{2}R

\gamma=\frac{C_P}{C_V}=\frac{\frac{7}{2}R}{\frac{5}{2}R}=1.40, অর্থাৎ দ্বিপারমাণবিক গ্যাসের ক্ষেত্রে \gamma=1.40

বহুপারমাণবিক গ্যাসের ক্ষেত্রে (Specific Heat for Polyatomic Gas)

C_V=3R এবং

C_P=3R+R=4R

\gamma=\frac{C_P}{C_V}=\frac{4R}{3R}=1.33, অর্থাৎ বহুপারমাণবিক গ্যাসের ক্ষেত্রে \gamma=1.33

সকল এক পরমাণুক গ্যাসের ক্ষেত্রে [যেমন He, Ne, Ar] \gamma–এর মান 1.67। সকল দ্বিপরমাণুক গ্যাসের ক্ষেত্রে [ যেমন H_2, O_2, N_2, Cl_2] \gamma] –এর মান 1.40 এবং সকল ত্রিপরমাণুক গ্যাসের ক্ষেত্রে [ যেমন CO_2, C_2H_6, NH_3] \gamma–এর মান 1.33। অতএব একই প্রকার আণবিক গঠনের জন্য \gamma–এর মান নির্দিষ্ট এবং বিভিন্ন গঠনের গ্যাসের জন্য \gamma– এর মান ভিন্ন ভিন্ন হয়।

\gamma–এর গুরুত্ব (Importance of Specific Heat):

(ক) কোনো গ্যাসের \gamma–এর মান জানা থাকলে ওই গ্যাসের আণবিক বিন্যাস জানা যায় অর্থাৎ ওই গ্যাসের প্রতিটি অণুর মধ্যে কয়টি পরমাণু আছে তা জানা যা।

(খ) গ্যাসীয় মাধ্যমের শব্দের বেগ \gamma–এর মানের ওপর নির্ভর করে। তাই শব্দের বেগ নির্ণয়ের জন্য এর প্রয়োজন হয়।

(গ) গ্যাসের রুদ্ধতাপ প্রক্রিয়া পর্যালোচনার জন্য \gamma–এর মান জানা দরকার।

রুদ্ধতাপীয় রেখা (লেখ) সমোষ্ণ রেখা (লেখ)-এর চেয়ে অধিকতর খাড়া (Adiabatic Curve is more Steeper than Isothermal Curve)

P-V লেখচিত্রের সাহায্যে সমোষ্ণ ও রুদ্ধতাপীয় প্রক্রিয়া নির্দেশ করা যায়। লেখচিত্রের কোনো বিন্দুতে স্পর্শক টানলে ওই বিন্দুতে ঢাল বা নতি হবে \frac{dP}{dV}। দেখা যায় যে, যেকোনো বিন্দুতে রুদ্ধতাপ রেখার ঢাল সমোষ্ণ রেখার ঢালের \gamma গুণ হয়।

সমোষ্ণ ও রুদ্ধতাপীয় সমীকরণদ্বয়কে ব্যবকলন করে সহজেই প্রমাণ করা যায় যে রুদ্ধতাপীয় রেখা সমোষ্ণ রেখা অপেক্ষা \gamma-গুণ খাড়া।

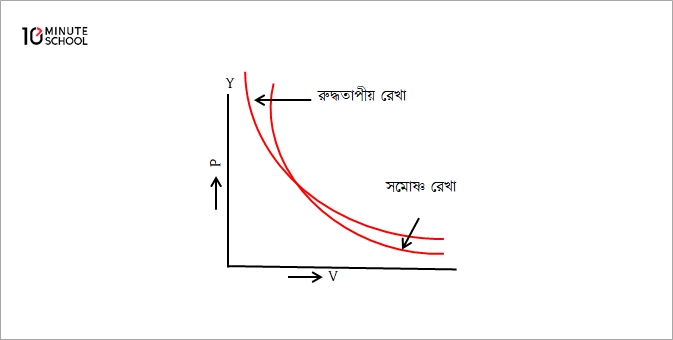
সমোষ্ণ পরিবর্তনের ক্ষেত্রে

PV= ধ্রুবক

উভয় পক্ষকে ব্যবকলন করে পাই, PdV+VdP=0

বা,\Big(\frac{dP}{dV}\Big)_{সমোষ্ণ}=-\frac{P}{V} ——————- (1.8)

অপরপক্ষে, রুদ্ধতাপ পরিবর্তনের ক্ষেত্রে, PV^{\gamma}= ধ্রুবক

উভয় পক্ষকে ব্যবকলন করে পাই,

\gamma PV^{(\gamma-1)}dV+V^{\gamma}dP=0

বা, \Big(\frac{dP}{dV}\Big)_{রুদ্ধতাপ}=-\frac{\gamma P V^{\gamma-1}}{V^</span>{\gamma}}——————- (1.9)

সমীকরণ 1.8 ও 1.9 তুলনা করলে দেখা যায় যে,

\Big(\frac{dP}{dV}\Big)_{রুদ্ধতাপ}=\Big(\frac{dP}{dV}\Big)</span></span>_{সমোষ্ণ}

বা, \frac{\Big(\frac{dP}{dV}\Big)_{রুদ্ধতাপ}}{\Big(\frac{dP}{dV}\Big)_{সমোষ্ণ}}=\gamma

সুতরাং, যে কোনো বিন্দুতে রুদ্ধতাপ রেখার ঢাল ওই বিন্দুতে সমোষ্ণ রেখার ঢাল অপেক্ষা \gamma গুণ বেশি।

যেহেতু যে কোনো গ্যাসের ক্ষেত্রে \gamma>1, সুতরাং রুদ্ধতাপীয় রেখা সমোষ্ণ রেখার চেয়ে \gammaগুণ খাড়া।