উল্লম্ব গতির ক্ষেত্রে ত্বরণ সম্পর্কিত সূত্রসমূহের প্রয়োগ | Application of formulae related to acceleration in case of vertical motion

কোনো বস্তুকণাকে উপর থেকে ছেড়ে দিলে অভিকর্ষজ বলের প্রভাবে ভূ-পৃষ্ঠে পড়ে। অভিকর্ষজ বল ক্রিয়ারত থাকায় বস্তুকণাটির একটি সুষম ত্বরণ থাকে। এ ত্বরণকে বলা হয় অভিকর্ষজ ত্বরণ। উল্লম্ব গতির ক্ষেত্রে এই অভিকর্ষজ ত্বরণকে g দ্বারা প্রকাশ করা হয়। পরীক্ষা করে দেখা গেছে ভূ পৃষ্ঠে g এর মান 9.8 m/sec^2 কোনো বস্তুকণা ঊর্ধ্বে নিক্ষেপ করলে অভিকর্ষ বলের প্রভাবে বেগ কমতে থাকে বলে সেক্ষেত্রে অভিকর্ষজ ত্বরণ g এর মান ঋণাত্মক ধরা হয়।

১৬০০ খ্রিস্টাব্দের শেষের দিকে প্রথম বারের মত বিজ্ঞানী গ্যালিলিও তাত্ত্বিকভাবে প্রমাণ করেন যে বায়ুহীন কোনো স্থানে বিভিন্ন ভরের ও আকারের বস্তু একই সময়ে ছেড়ে দিলে এরা একই সময়ে ভূমিতে পড়ে। বিজ্ঞানী নিউটন 1 মিটার বায়ুশূন্য টিউবে গিনি ও পালক নিয়ে পরীক্ষা করে দেখান যে গিনি ও পালক একই সময়ে ছেড়ে দিলে টিউবের তলায় একই সময়ে পৌঁছে।

অভিকর্ষজ ত্বরণের মান (Magnitude of acceleration due to gravity):

C.G.S. পদ্ধতিতে g এর মান 981 সে.মি./সেকেন্ড^2, M.K.S. পদ্ধতিতে 9.81 মিটার/সেকেন্ড^2 এবং F.P.S. পদ্ধতিতে 32 ফুট/সেকেন্ড^2। বিষুব অঞ্চলে g এর মান মেরু অঞ্চল হতেও কম। মেরু অঞ্চলে এর মান সবচেয়ে বেশি। ভূ-কেন্দ্রে এর মান শূন্য। আবার, ভূ-পৃষ্ঠ হতে যত উপরের দিকে উঠা হয় বা নিচের দিকে যত নামা হয়, g এর মান ততই কমতে থাকে। 

উল্লম্ব রেখায় চলমান বস্তুর অতিক্রান্ত দূরত্বকে h এবং অভিকর্ষজ ত্বরণকে g দ্বারা প্রকাশ করা হয়। এক্ষেত্রে গতির সমীকরণগুলি নিম্নরূপ:

উচ্চস্থান হতে অবাধে পতনশীল বস্তুর ক্ষেত্রে u=0	ভূমি হতে u আদিবেগে বস্তুটি খাড়া উপরে নিক্ষিপ্ত হলে	নির্দিষ্ট h উচ্চতা হতে u বেগে নিচের দিকে নিক্ষিপ্ত হলে	h উচ্চতা হতে u আদিবেগে উপরে নিক্ষিপ্ত হলে
v=g t	v=u-g t	v=u+g t	v=-u+g t
h=\frac{1}{2} g t^{2}	h=u t-\frac{1}{2} g t^{2}	h=u t+\frac{1}{2} g t^{2}	h=-u t+\frac{1}{2} g t^{2}
v^{2}=2 g h	v^{2}=u^{2}-2 g h	v^{2}=u^{2}+2 g h	v^{2}=u^{2}+2 g h
h_{t h}=\frac{1}{2} g(2 t-1)	h_{t h} =u-\frac{1}{2} g(2 t-1)	h_{t h} =u+\frac{1}{2} g(2 t-1)	h_{t h}  =-u+\frac{1}{2} g(2 t-1)

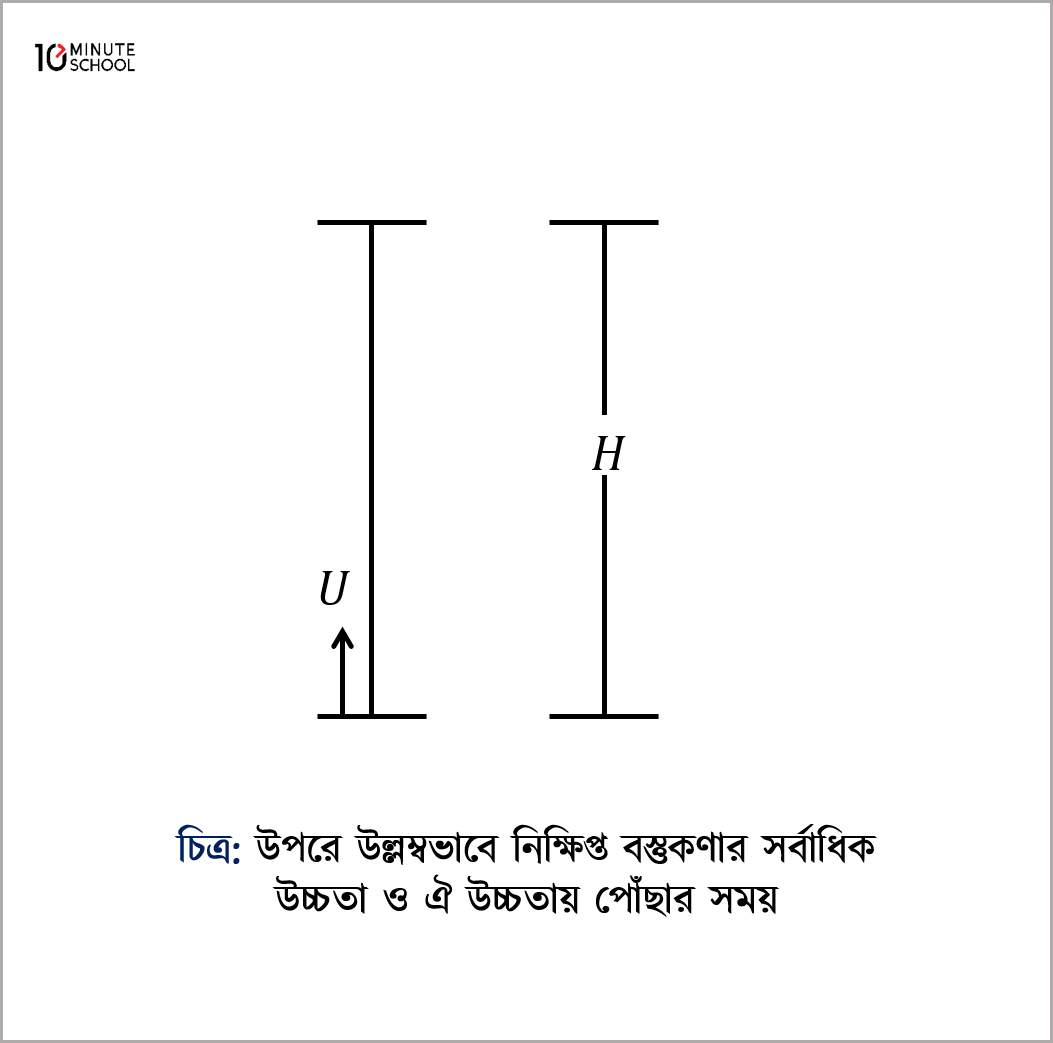
উপরে উল্লম্বভাবে নিক্ষিপ্ত বস্তুকণার সর্বাধিক উচ্চতা ও ঐ উচ্চতায় পোঁছার সময়:

u আদিবেগে একটি বস্তুকণাকে ভূমি থেকে খাড়া উপরের দিকে নিক্ষেপ করলে অভিকর্ষজ ত্বরণ প্রতিকূলে কাজ করে বলে g মন্দনের সৃষ্টি হয় ফলে বস্তুকণাটির বেগ ক্রমশঃ কমতে থাকে। T_{1} সময়ে সর্বাধিক H উচ্চতায় বস্তুকণাটির বেগ শূন্য হবে।

\therefore 0=u^{2}-2 g H \quad\left[v^{2}=u^{2}-2 g h\right. সূত্রের সাহায্যে]

বা, 2 g H=u^{2}

\therefore H=\frac{u^{2}}{2 g}= সর্বাধিক উচ্চতা 

এবং 0=u-g T_{1} \quad[\because v=u-g t]

বা, g T_{1}=u

\therefore T_{1}=\frac{u}{g}= উত্থানকাল  

যদি বস্তুকণাটি T_{2} সময়ে অভিকর্ষজ ত্বরণে পুনরায় ভূমিতে ফিরে আসে তবে,

H=0+\frac{1}{2} g T_{2}{ }^{2}

বা, \frac{u^{2}}{2 g}=\frac{1}{2} g T_{2}{ }^{2} \quad\left[\because H=\frac{u^{2}}{2 g}\right]

বা, g^{2} T_{2}{ }^{2}=u^{2}

বা, T_{2}{ }^{2}=\frac{u^{2}}{g^{2}}

\therefore T_{2}=\frac{u}{g}= পতনকাল

∴ উত্থানকাল = পতনকাল 

অর্থাৎ কোনো বস্তুকণা খাড়া উপরের দিকে নিক্ষেপ করলে উত্থানকাল ও পতনকাল সমান।

আবার, কোনো বস্তুকণা উল্লম্বভাবে উপরের দিকে নিক্ষেপ করলে নিক্ষেপের পর হতে সর্বোচ্চ বিন্দুতে উঠার পর পুনরায় ভূমিতে ফিরে আসতে যে সময় লাগে তাকে বিচরণ কাল (Time of flight) বলা হয়। 

মোট বিচরণকাল T হলে, T=T_{1}+T_{2}=\frac{u}{g}+\frac{u}{g}=\frac{2 u}{g}

∴ মোট বিচরণকাল =\frac{2 u}{g}

মাধ্যাকর্ষণের প্রভাবে বস্তুর উল্লম্বগতি (Vertical motion under gravity)

u বেগে খাড়া উর্ধ্ব দিকে নিক্ষিপ্ত কোনো বস্তুকণার গতি: 

খাড়া উর্ধ্ব দিককে ধনাত্মক ধরে ত্বরণ \frac{d^{2} s}{d t^{2}}=-g।

যোগজীকরণ করে পাই, \frac{d s}{d t}=-g t+A \quad ... \quad ...(1)

আদি অবস্থায় যখনt=0, তখন বেগ \frac{d s}{d t}=u

\therefore (1) নং হতে পাই, A=u

সমীকরণ (1) এর A=u বসিয়ে পাই, \frac{d s}{d t}=-g t+u \quad ... \quad ...(2)

যদি t সময়ে কণাটির বেগ y হয় অর্থাৎ \frac{d s}{d t}=v  হয়, তবে (2) হতে পাই, v=u-g t \quad ... \quad ...(3)

এখন (t) এর সাপেক্ষে সমীকরণ (2) কে যোগজীকরণ করে পাই, s=u t-\frac{1}{2} g t^{2}+B \quad ... \quad ...(4)

আদি অবস্থায় যখন t=0, তখন s=0 ফলে B=0

∴(4) হতে পাই, s=u t-\frac{1}{2} g t^{2} \quad ... \quad ...(5)

(5) এ s এর পরিবর্তে উচ্চতাকে h দ্বারা প্রকাশ করে পাই, h=u t-\frac{1}{2} g t^{2} \quad ... \quad ...(6)

এখন ত্বরণ \frac{d^{2} s}{d t^{2}}=-g \Rightarrow \frac{d}{d t}\left(\frac{d s}{d t}\right)=-g \Rightarrow \frac{d v}{d t}=-g, \quad\left[\because \frac{d s}{d t}=v\right]

\Rightarrow \frac{d v}{d s} \cdot \frac{d s}{d t}=-g \Rightarrow \frac{d v}{d s} \cdot v=-g \Rightarrow v d v=-g d s \quad ... \quad ...(7)

যখন s=0, তখন v=u এবং যখন s=s তখন v=v । এ সীমার মধ্যে সমীকরণ (7) এর উভয় পক্ষকে যোগজীকরণ করে পাই,  

\int_{u}^{v} v d v=-g \int_{0}^{s} d s

\Rightarrow\left[\frac{v^{2}}{2}\right]_{u}^{v}=-g[s]_{0}^{s}

\Rightarrow \frac{v^{2}}{2}-\frac{u^{2}}{2}=-g(s-0)

\therefore v^{2}=u^{2}-2 g s \quad ... \quad ...(8)

সমীকরণ (8) এ s এর পরিবর্তে উচ্চতাকে h দ্বারা প্রকাশ করে পাই, v^{2}=u^{2}-2 g h \quad ... \quad ...(9)

h উচ্চতা হতে অবাধে পতনশীল বস্তুর গতি:

মনে করি, h উচ্চতা থেকে কোনো বস্তু মাধ্যাকর্ষণজনিত ত্বরণের প্রভাবে অবাধে পতিত হয়ে t সময়ে ভূমিতে v বেগে আঘাত করে। অবাধে পতনশীল বস্তুর ক্ষেত্রে আদিবেগ u=0

\therefore h=0 \times t+\frac{1}{2} g t^{2} \Rightarrow t^{2}=\frac{2 h}{g} \Rightarrow t=\sqrt{\frac{2 h}{g}} \ldots .(i)

এবং v^{2}=0+2 g h \quad \therefore v=\sqrt{2 g h} \ldots \ldots (ii); যেহেতু নিচের দিকে গতির ক্ষেত্রে বেগ ধনাত্মক। 

(i) ও (ii) থেকে বলা যায়, h উচ্চতা হতে অবাধ পতনশীল বস্তু \sqrt{2 h / g} সময় পরে \sqrt{2 g h} বেগে ভূমিতে আঘাত করে। 

দ্রষ্টব্য: পূর্বের অনুচ্ছেদগুলোতে আমরা পেয়েছি, v=u+f t, s=u t+\frac{1}{2} f t^{2}, v^{2}=u^{2}+2 f s

এখানে f=-g ও s=h পরিবর্তন করে পাই, v=u-g t, h=u t-\frac{1}{2} g t^{2}, v^{2}=u^{2}-2 g h। 

u বেগে খাড়া নিম্ন দিকে নিক্ষিপ্ত কোনো বস্তুকণার গতির ক্ষেত্রে, ত্বরণ =\frac{d^{2} s}{d t^{2}}=g

উপরিউক্ত পদ্ধতিতে দেখানো যাবে, v=u+g t, h=u t+\frac{1}{2} g t^{2}, v^{2}=u^{2}+2 g h.

উদাহরণ-১: একটি পাথর কুয়ার ভিতর ফেলার t সময় পরে পানিতে এর পতন শব্দ শোনা গেল। শব্দের বেগ v এবং কুয়ার গভীরতা h হলে, বাতাসের বাধা অগ্রাহ্য করে প্রমাণ কর যে,

t=\sqrt{\frac{2 h}{g}}+\frac{h}{v}

g v^{2} t^{2}-2 g h v+h\left(g h-2 v^{2}\right)=0

g t^{2}=2 h\left(1+\frac{g t}{v}\right) , যখনv>h

সমাধান: মনে করি, পাথরটি t_{1} সময়ে কুয়ার পানিতে পতিত হয় এবং সেখান থেকে পতন শব্দ কুয়ার উপরিভাগে আসতে t_{2} সময় লাগে। তাহলে, t=t_{1}+t_{2} \quad ... \quad ...(i)

পাথর পতনে ক্ষেত্রে, h=0 \times t_{1}+\frac{1}{2} g t_{1}^{2} \Rightarrow g t_{1}^{2}=2 h \Rightarrow t_{1}=\sqrt{\frac{2 h}{g}}

শব্দের ক্ষেত্রে, h=v t_{2} \Rightarrow t_{2}=\frac{h}{v}

(i) নং এ t_{1} ও t_{2} এর মান বসিয়ে পাই, t=\sqrt{\frac{2 h}{g}}+\frac{h}{v} (Proved)

\Rightarrow t-\frac{h}{v}=\sqrt{\frac{2 h}{g}} \Rightarrow t^{2}-\frac{2 h t}{v}+\frac{h^{2}}{v^{2}}=\frac{2 h}{g} \quad ... \quad ...(i i) [বর্গ করে]

\therefore g v^{2} t^{2}-2 g h v t+g h^{2}=2 h v^{2} (Proved)

শব্দের বেগ v>h । সুতরাং \frac{h^{2}}{v^{2}} কে অতি ক্ষুদ্র বিবেচনা করে অগ্রাহ্য করা যায়। 

\therefore t^{2}-\frac{2 h t}{v}=\frac{2 h}{g} \Rightarrow g t^{2}-\frac{2 g h t}{v}=2 h \Rightarrow g t^{2}=2 h\left(1+\frac{g t}{v}\right) (Proved) 

ভূমিতে বস্তুর পতনবেগ:

মনে করি, ভূমি হতে u আদি বেগে একটি বস্তু উল্লম্বভাবে উপরের দিকে নিক্ষেপ করা হল। সর্বাধিক H উচ্চতায় বস্তুটির বেগ শূন্য হয় এবং অতঃপর তাৎক্ষণিকভাবে বস্তুটি উল্লম্বভাবে নিচের দিকে পড়তে থাকে। বস্তুটি v বেগে ভূমিকে আঘাত করলে,

v^{2}=u^{2}+2 g h হতে পাই, v^{2}=0+2 g H=2 g \times \frac{u^{2}}{2 g}=u^{2}

\Rightarrow|v|=u

∴ উত্থান বেগ = |পতন বেগ|

ভূমির উর্ধ্বে h উচ্চতা থেকে u বেগে উল্লম্বভাবে উপরে নিক্ষিপ্ত একটি বস্তুকণা t সময়ে v বেগে পতিত হলে, (i) \quad v=-u+g t (ii) \quad h=-u t+\frac{1}{2} g t^{2}

মনে করি, ভূমির ঊর্ধ্বে AB=h উচ্চতায় B বিন্দু থেকে u আদি বেগে উল্লম্বভাবে উপরের দিকে নিক্ষেপ বস্তুকণাটি t_{1} সময় পর সর্বোচ্চবিন্দু C তে পৌঁছে এবং বেগ শূন্য হয়।

\therefore 0=u-g t_{1} \Rightarrow t_{1}=\frac{u}{g}

এবং B C=\frac{u^{2}}{2 g} [∵ সর্বাধিক উচ্চতা =\frac{u^{2}}{2 g}] 

ধরি, বস্তুটি B বিন্দু থেকে t সময় পর ভূমির A বিন্দুতে আঘাত করে। তাহলে বস্তুটি C হতে শূন্য আদিবেগে (t-t_{1}) সময়ে CA দূরত্ব অতিক্রম করে।

\therefore A C=0+\frac{1}{2} g\left(t-t_{1}\right)^{2}=\frac{1}{2} g\left(t-\frac{u}{g}\right)^{2}=\frac{1}{2} g\left(t^{2}-2 \frac{u}{g} t+\frac{u^{2}}{g^{2}}\right)=\frac{1}{2} g t^{2}-u t+\frac{u^{2}}{2 g}

\therefore h=-u t+\frac{1}{2} g t^{2}

আবার, বস্তুটি C হতে শূন্য আদিবেগে (t-t_{1}) সময় পর ভূমিকে v বেগে আঘাত করলে, 

v=0+g\left(t-t_{1}\right)=g\left(t-\frac{u}{g}\right)=g t-u

\therefore v=-u+g t

নির্দিষ্ট কোনো উচ্চতায় বস্তুকণার বেগ ও সময় (Time and velocity of a particle to a given height)  

O বিন্দু থেকে u আদিবেগে উল্লম্বভাবে নিক্ষিপ্ত বস্তুকণা h উচ্চতায় v বেগ অর্জন করে। 

\therefore v^{2}=u^{2}-2 g h বা, v=\pm \sqrt{u^{2}-2 g h}

\therefore h উচ্চতায় গতিবেগ =\pm \sqrt{u^{2}-2 g h}

\pm চিহ্নের দ্বারা h উচ্চতায় কোন বস্তুকণার দুইটি সমমানের কিন্তু বিপরীতমুখী বেগ অর্থাৎ উঠন্ত অবস্থায় বেগ \sqrt{u^{2}-2 g h} এবং পড়ন্ত অবস্থায় বেগ  -\sqrt{u^{2}-2 g h} বুঝায়।

আবার, মনে করি বস্তুকণাটি O বিন্দু থেকে u আদিবেগে খাড়াভাবে নিক্ষিপ্ত হলো এবং উহা g মন্দনে t সময়ে h উচ্চতায় পৌঁছে।

h=u t-\frac{1}{2} g t^{2} বা, 2 h=2 u t-g t^{2}

বা, g t^{2}-2 u t+2 h=0 বা, t=\frac{2 u \pm \sqrt{(-2 u)^{2}-4 . g .2 h}}{2 . g}

=\frac{2 u \pm \sqrt{4\left(u^{2}-2 g h\right)}}{2 . g}

=\frac{u \pm \sqrt{u^{2}-2 g h}}{g}

=\frac{u}{g} \pm \frac{\sqrt{u^{2}-2 g h}}{g}

u^{2}-2 g h>0 হলে t এর বাস্তব দুটি মান পাওয়া যাবে।

∴ খাড়াভাবে নিক্ষিপ্ত বস্তু দুইবার নির্দিষ্ট h উচ্চতায় অবস্থান করে।

t এর ক্ষুদ্রতম মান \frac{u}{g}-\frac{\sqrt{u^{2}-2 g h}}{g} দ্বারা বস্তুকণাটি উঠন্ত অবস্থায় t এর বৃহত্তম \frac{u}{g}+\frac{\sqrt{u^{2}-2 g h}}{g} দ্বারা বস্তুটি পড়ন্ত অবস্থায় h উচ্চতায় গমন কালকে নির্দেশ করে

বিশেষ দ্রষ্টব্য: একটি শূন্য কূপের মধ্যে একটি ঢিল ফেলার t সে. পরে কূপের তলদেশে ঢিল পড়ার শব্দ শোনা গেল। শব্দের বেগ v হলে কূপের গভীরতা, h=\frac{g t^{2}}{2\left(1+\frac{g t}{v}\right)} (বহুনির্বাচনীর ক্ষেত্রে প্রযোজ্য)

বায়ুশূন্য অবস্থায় উল্লম্ব তলে প্রক্ষিপ্ত বস্তুকণার গতিপথ একটি প্যারাবোলা (The path of a projectile in vacuous is a parabola)

মনে করি, একটি বস্তুকণা O বিন্দু থেকে u আদিবেগে আনুভূমিকের সঙ্গে \alpha কোণে প্রক্ষিপ্ত হলো। O বিন্দুগামী আনুভূমিক ও উল্লম্ব OX ও OY রেখাদ্বয়কে যথাক্রমে x-অক্ষ ও y-অক্ষ ধরলে t সময়ে বস্তুকণাটি P(x,y) বিন্দুতে অবস্থান করে। O বিন্দুতে u এর আনুভূমিক লম্বাংশ u \cos \alpha এবং উল্লম্ব লম্বাংশ u \sin \alpha । আনুভূমিকের দিকে অভিকর্ষজ ত্বরণ শূন্য।

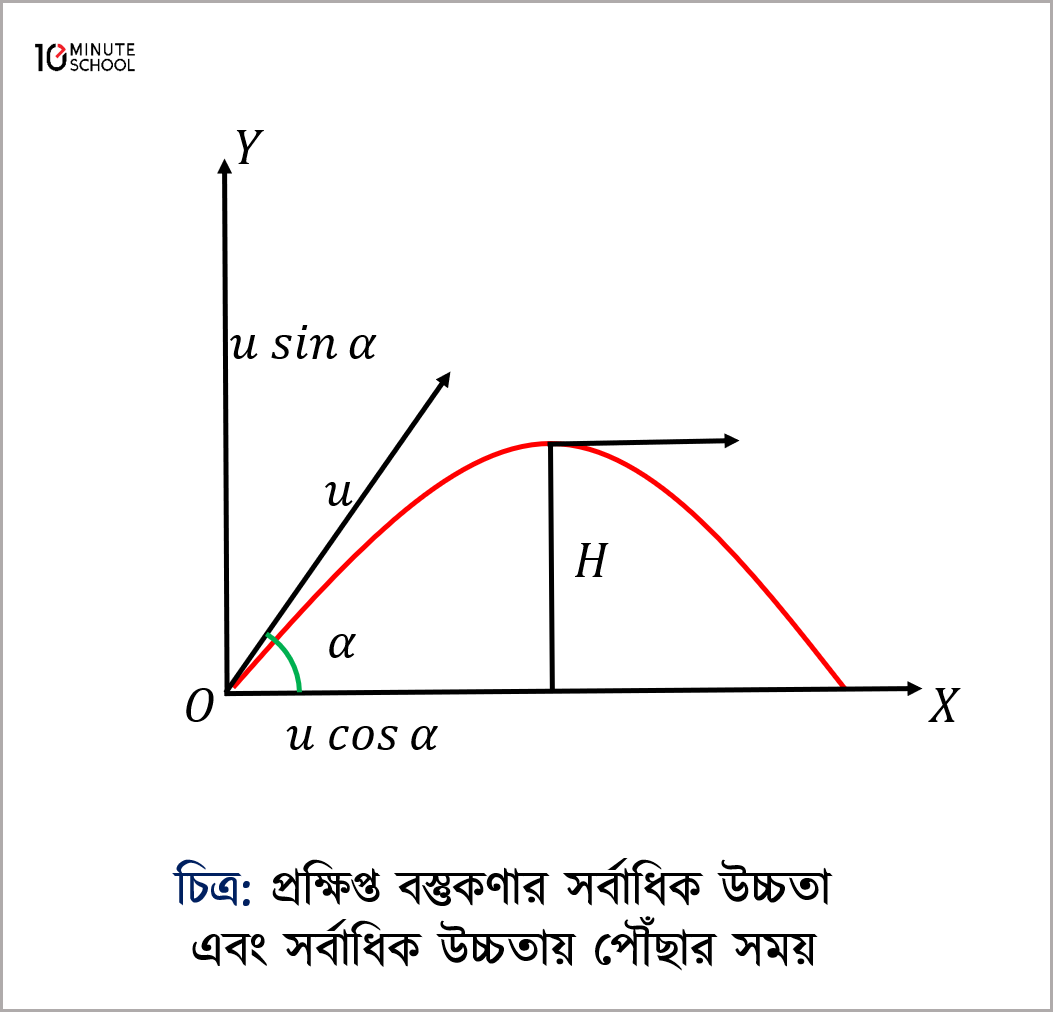
t সময়ে আনুভূমিক সরণ x=u \cos \alpha \cdot t \quad \therefore t=\frac{x}{u \cos \alpha}

t সময়ে উল্লম্ব সরণ y=u \sin \alpha \cdot t-\frac{1}{2} g t^{2} \quad ... \quad ...(i)

(i) এ t এর মান বসিয়ে পাই, 

y=u \sin \alpha \cdot \frac{x}{u \cos \alpha}-\frac{1}{2} g \frac{x^{2}}{u^{2} \cos ^{2} \alpha}=x \tan \alpha-\frac{g x^{2}}{2 u^{2} \cos ^{2} \alpha} \quad ... \quad ...(ii)

u,\alpha,g ধ্রুবক বলে a=-\frac{g}{2 u^{2} \cos ^{2} a} এবং b=\tan \alpha ধরে পাই, y=a x^{2}+b x, যা t মুক্ত।

∴ বায়ুশূন্য স্থানে আনুভূমিকের সাথে তির্যকভাবে নিক্ষিপ্ত বস্তুর গতিপথ প্যারাবোলা।

অনুসিদ্ধান্ত: বায়ুহীন অবস্থায় অনুভূমিকের সাথে \alpha কোণে শূন্যে নিক্ষিপ্ত বস্তুর আনুভূমিক পাল্লা R হলে, এর গতিপথের সমীকরণ, y=x \tan \alpha\left(1-\frac{x}{R}\right)

(ii) নং হতে পাই, 

y=x \tan \alpha-\frac{g x^{2}}{2 u^{2} \cos ^{2} \alpha}=x \tan \alpha-\frac{g x^{2} \tan \alpha}{2 u^{2} \sin a \cos \alpha}

=x \tan \alpha\left(1-\frac{g x}{u^{2} \sin 2 \alpha}\right)=x \tan \alpha\left(1-\frac{x}{\frac{u^{2} \sin 2 \alpha}{g}}\right)=x \tan \alpha\left(1-\frac{x}{R}\right)

ভূমি হতে উচ্চ কোনো স্থান থেকে আনুভূমিকে নিক্ষিপ্ত কোনো বস্তুকণার গতিপথ একটি প্যারাবোলা:

মনে করি, একটি বস্তুকণাকে বায়ুশূন্য স্থানে নির্দিষ্ট উচ্চতায় O বিন্দু থেকে u আদিবেগে আনুভূমিকভাবে নিক্ষেপ করা হলো। OX কে x-অক্ষ ও OY কে y-অক্ষ ধরলে t সময়ে বস্তুকণাটি P(x,-y) বিন্দুতে অবস্থান করে। O বিন্দুতে u এর আনুভূমিক লম্বাংশ u \cos 0^{\circ}বা u এবং উল্লম্ব u \sin 0^{\circ} বা 0। আনুভূমিক দিকে অভিকর্ষজ ত্বরণ শূন্য।

t সময়ে আনুভূমিক সরণ x=u \cos 0^{\circ} \cdot t=u t

\therefore t=\frac{x}{u} \ldots \ldots(i)

t সময়ে উল্লম্ব সরণ -y=+u \sin 0^{\circ} t-\frac{1}{2} g t^{2} বা, -y=0-\frac{1}{2} g t^{2} বা, y=\frac{1}{2} g t^{2}

(i) নং হতে t এর মান বসিয়ে, y=\frac{1}{2} g \cdot \frac{x^{2}}{u^{2}} বা, x^{2}=\frac{2 u^{2}}{g} y

u এবং g ধ্রুবক বলে \frac{2 u^{2}}{g}=4 a ধরে পাই, x^{2}=4 a y, যা পরাবৃত্তের সমীকরণ। 

∴ ভূমি হতে উচ্চ কোনো স্থান হতে আনুভূমিকভাবে নিক্ষিপ্ত বস্তুকণার গতিপথ একটি প্যারাবোলা।

বি.দ্র. বহুনির্বাচনি প্রশ্ন সমাধানের জন্য কিছু বিশেষ কৌশল নিম্নে দেওয়া হলো: 

• একটি বস্তুকে ভূমি থেকে কোণে এমনভাবে নিক্ষেপ করা হলো যেন তা 2a ব্যবধানে অবস্থিত a পরিমাণ উঁচু দুইটি দেয়ালের ঠিক উপর দিয়ে অতিক্রম করে। বস্তুটির আনুভূমিক পাল্লা R হলে, R=2 a \cot \frac{\alpha}{2}
• একটি বস্তু u মি./সে. বেগে ভূমির সাথে কোণে নিক্ষিপ্ত হলো। t সময় পর বস্তুটি নিক্ষেপ দিকের সাথে লম্বভাবে চললে, t=\frac{u}{g \sin \alpha} এবং এ সময়ে বেগ, v=u \cot \alpha.