হাইগেনস-এর নীতি (Huygens’s principle )

হাইগেনস-এর  নীতিতে আলাকে তরঙ্গের বিস্তার কৌশল
(Propagation of light waves on the basis of Huygens’s principle)

ধারণা (Concept) : 

উৎস জানা থাকলে সাধারণ নিয়মে তরঙ্গমুখের যে কোনো সময়ের অবস্থান নির্ণয় করা যায়। উৎস জানা না থাকলেও কোনো এক সময়ের তরঙ্গমুখের অবস্থান ও আকৃতি জানা থাকলে হাইগেনস-এর নীতি (Huygens’s principle) অনুসরণ করে অন্য যে কোনো সময়ে তরঙ্গমুখের অবস্থান ও আকৃতি নির্ণয় করা যায়। হাইগেনস-এর নীতি (Huygens’s principle) অনুসারে তরঙ্গমুখের প্রতিটি বিন্দুকে গালোকীয় তরঙ্গের উৎস হিসেবে গণ্য করা যায়। এসব তরঙ্গকে গৌণ তরঙ্গ (secondary waves) বলে। গৌণ তরঙ্গগুলো মূল তরঙ্গের সমান বেগে সামনের দিকে অগ্রসর হয়। হাইগেনস-এর নীতিকে আমরা নিম্নোক্তভাবে বিবৃত করতে পারি।

বিবৃতি : কোনো একটি তরঙ্গমুখের ওপর অবস্থিত প্রতিটি বিন্দু এক একটি অণু তরঙ্গের বা গৌণ তরঙ্গের উৎস হিসেবে বিবেচিত হয়। ওই গৌণ উৎসগুলো থেকে সৃষ্ট তরঙ্গমালা মূল তরঙ্গের সমান বেগে সামনের দিকে অগ্রসর হয়। যে কোনো সময়ে ওই সব গৌণ তরঙ্গমালাকে স্পর্শ করে একটি তল অঙ্কন করলে ওই তলই ওই সময়ের তরঙ্গমুখের নতুন অবস্থান নির্দেশ করে।)

হাইগেনস-এর নীতি অনুসারে তরমুখ-এর অবস্থান
(Position of wave front according to Huygens’s principle) 

চিত্র -এ যথাক্রমে সমতল তরঙ্গের ক্ষেত্রে এবং গোলকীয় তরঙ্গের ক্ষেত্রে গৌণ তরঙ্গমুখ এবং তরঙ্গমুখের নতুন অবস্থান দেখানো হয়েছে। মনে করি, কোনো সমসত্ত্ব মাধ্যমে P একটি বিন্দু আলোক উৎস । P-এর অণুগুলোর কম্পনে উৎপন্ন তরঙ্গ চারদিকে ছড়িয়ে পড়েছে। কোনো এক সময়ে তরঙ্গমুখের অবস্থান AB।

হাইগেনস-এর নীতি (Huygens’s principle) অনুসারে t সময়ে তরঙ্গমুখের অবস্থান বের করতে হবে। তরঙ্গমুখের AB অবস্থানে 5টি বিন্দু 1, 2, 3, 4 ও 5 ধরা হলো। (এরূপ অসংখ্য বিন্দু কল্পনা করা যায়।) হাইগেনস-এর নীতি (Huygens’s principle) অনুসারে প্রতিটি বিন্দু নতুন আলোড়নের উৎস হিসেবে ক্রিয়া করে নতুন তরঙ্গ সৃষ্টি করবে। 

(ক) সমতল তরঙ্গের বেলায়; (খ) গোলকীয় তরঙ্গের বেলায়

আলোকের বেগ υ হলে t সময়ে তরঙ্গগুলি υt দূরত্ব অতিক্রম করবে। বিন্দুগুলিকে কেন্দ্র ধরে υt ব্যাসার্ধ নিয়ে বৃত্তচাপ আঁকি। চাপগুলোর একটি সাধারণ স্পর্শক CD আঁকি। এখন CD হলো তরঙ্গমুখের নতুন অবস্থান। বিন্দুগুলি হতে অঙ্কিত বৃত্ত বা গোলকীয় চাপই হলো গৌণ উৎস হতে উৎপন্ন তরঙ্গের t সময় পরের অবস্থান। এখানে উল্লেখ্য যে, ত্রিমাত্রিক স্থানে বিন্দুগুলো t ব্যাসার্ধের গোলকীয় চাপ রচনা করবে। ওই চাপগুলোর একটি সাধারণ স্পর্শক বা মোড়ক (envelope) CD একটি গোলীয় তল হবে।

সময়ের সাথে সাথে আলোক তরঙ্গ দূরে সরে যাবে এবং গোলীয় তলের বক্রতা কমতে থাকবে। বহু দূরে একে সমতল ধরা যায়।

চিত্র -এ অসীম দূর হতে আগত তরঙ্গমুখের কোনো এক সময়ের অবস্থান AB দেখানো হয়েছে। এই তরঙ্গমুখের ওপর কয়েকটি বিন্দু নিয়ে ওপরের নিয়মে t ব্যাসার্ধ নিয়ে বৃত্ত গোলীয় চাপ এঁকে একটি সাধারণ স্পর্শক CD আঁকলে CD হবে তরঙ্গমুখের নতুন অবস্থান। হাইগেনসের নীতি (Huygens’s principle) অনুসারে এটি সমতল তরঙ্গমুখ নির্দেশ করে।

সংজ্ঞা : কোনো তরঙ্গের উপর অবস্থিত সমদশাসম্পন্ন কণাগুলোর গতিপথকে তরঙ্গমুখ বলে। তরঙ্গমুখের ওপর অঙ্কিত অভিলম্বকে রশ্মি (ray) বলা হয়। তরঙ্গের শক্তি এই রশ্মি বরাবর শূন্যস্থান বা মাধ্যমের এক অংশ থেকে অন্য অংশে স্থানান্তরিত হয়।

হাইগেনসের নীতির ভিত্তিতে আলোর প্রতিফলন ও প্রতিসরণ

(The reflection and refraction of light based on Huygens’s Principle)

আলোর প্রতিফলন (Reflection of light) :

মনে করি, XY একটি সমতল প্ৰতিফলক তল। a, b, c তিনটি সমান্তরাল আলোক রশ্মি। এরা তির্যকভাবে XY তলের ওপর আপতিত হলো [চিত্র ৭.৬]। ধরি, EPA এই সমান্তরাল রশ্মিগুলোর তরঙ্গমুখ। এর প্রত্যেকটি বিন্দু আলোড়ন কেন্দ্র হিসেবে ক্রিয়া করবে এবং ক্ষুদ্র ক্ষুদ্র গৌণ তরঙ্গ উৎপন্ন করবে। এই গৌণ তরঙ্গগুলো চারদিকে ছড়িয়ে পড়বে।

মনে করি A বিন্দু হতে একটি আলোক রশ্মি t সময়ে XY পৃষ্ঠের F বিন্দুতে পৌঁছবে। ফলে প্রতিফলিত তরঙ্গমুখ FMN পাওয়া যাবে। যদি বাতাসে আলোকের বেগ হয়, তবে FA = ot। এখন E-কে কেন্দ্র করে এবং FA = ot-কে ব্যাসার্ধ করে একটি বৃত্তচাপ অঙ্কন করলে FMN পাওয়া যাবে। FMN-এর স্পর্শক অঙ্কন করে নতুন তরঙ্গমুখ পাওয়া যাবে। এটিই হলো প্রতিফলিত তরঙ্গমুখ।

 

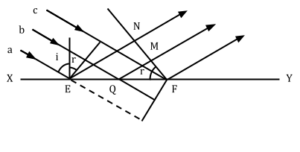
প্রতিফলনের সূত্রাবলি প্রমাণ :

\Delta AEF ও \Delta NEF-এর মধ্যে \angle EAF = \angle ENF = 1সমকোণ, AF = EN = ot  এবং EF তাদের সাধারণ বাহু।
∴ত্রিভুজদ্বয় সর্বসম এবং \angle AEF = \angle EFN                                                                                        
এখন আপতন বিন্দু E-তে EB লম্ব হলে,
\angle \alpha EB + \angle BEA = \angle BEA + \angle AEF = 1 সমকোণ
\therefore \angle \eta EB= \angle AEF = আপতন কোণ, \angle i                                                                                    
আবার, \angle \eta EB + \angle NEF = \angle EFN + \angle NEF = 1 সমকোণ
\therefore \angle NEB = \angle EFN = প্রতিফলন কোণ, \angle r                                                    
সমীকরণ হতে লেখা যায়, আপতন কোণ, \angle i = প্রতিফলন কোণ, \angle r । এ দ্বারা আলোকের প্রতিফলনের দ্বিতীয় সূত্র প্রমাণিত হলো।

আবার, আপতিত রশ্মি \alpha E , প্রতিফলিত রশি EN এবং আপতন বিন্দুতে অঙ্কিত অভিলম্ব EB কাগজের একই সমতলে অবস্থিত। এ দ্বারা আলোকের প্রতিফলনের প্রথম সূত্রটি প্রমাণিত হলো।

অতএব আলোকের তরঙ্গ তত্ত্বকে ভিত্তি করে হাইগেনস-এর নীতি অনুসারে (Huygens’s principle) প্রতিফলনের দুটি সূত্রই প্রমাণিত হলো।

আলোর প্রতিসরণ (Refraction of light): 

মনে করি, ‘a’ ও ‘b’ দুটি স্বচ্ছ সমসত্ত্ব মাধ্যম। XY এদের বিভেদতল। ধরি ‘a’ মাধ্যমে আলোকের বেগ v_a এবং ‘b’ মাধ্যমে আলোকের বেগ v_b ৷ এখানে v_a > v_b  । মনে করি d, e, f তিনটি সমান্তরাল রশ্মি। এরা তির্যকভাবে XY তলে আপতিত হলো । APE রশ্মিসমূহের তরঙ্গমুখ।
মনে করি, EPA তরমুখ প্রথমে বিভেদ তলের E বিন্দুতে স্পর্শ করে। হাইগেনস-এর নীতি অনুসারে ওই E বিন্দুতে অবস্থিত এর কণাটি আলোড়িত হয়ে গৌণ তরঙ্গ উৎপন্ন করে এবং ‘a’ ও ‘b‘ মাধ্যমে যথাক্রমে v_a , ও v_b বেগে ছড়িয়ে পড়ে। এখন A বিন্দু হতে আলোড়নটির F বিন্দুতে পৌছতে যদি t সময় লাগে তা হলে FA = v_at । উক্ত সময়ে E বিন্দুর আলোক তরঙ্গ ‘b’ মাধ্যমে EN দূরত্ব অতিক্রম করবে। অতএব EN = v_at  হবে।

A-কে কেন্দ্র করে এবং EN = v_bt -কে ব্যাসার্ধ করে একটি বৃত্তচাপ অঙ্কন করি এবং তার ওপর FN স্পর্শক টানলে FMN প্রতিসৃত তরঙ্গমুখ নির্দেশ করবে।

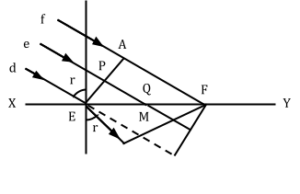
প্রতিসরণের সূত্রাবলি প্রমাণ : 

E বিন্দু দিয়ে XY-এর ওপর লম্ব BEB’ অঙ্কন করি।
এখন, \angle dEB + \angle BEA = \angle BEA + \angle AEF = 1  সমকোণ
\therefore \angle dEB = \angle AEF = আপতন কোণ, \angle i
আবার, \angle B^{\prime}EN + \angle NEF = \angle NEF + \angle EFN = 1  সমকোণ
\angle B^{\prime}EN = \angle EFN = প্রতিসরণ কোণ, \angle r

সুতরাং \frac{\sin i}{\sin r}=\frac{\sin \angle dEB}{\sin \angle B^{\prime}EN}=\frac{\sin \angle AEF}{\sin \angle EFN}   

             =\frac{AF/EF}{EN/EF}=\frac{AF}{EN}=\frac{v_{a} t}{v_{b} t}=\frac{v_{a}}{v_{b}}= একটি ধ্রুব সংখ্যা = a^{\mu}b

= a^{\mu}b হলো a মাধ্যম সাপেক্ষে b মাধ্যমের প্রতিসারঙ্ক।

এটি দ্বারা স্নেলের সূত্র বা প্রতিসরণের দ্বিতীয় সূত্রটি প্রমাণিত হলো। আবার আপতিত রশ্মি dE, প্রতিসৃত রশ্মি EN এবং আপতন বিন্দুতে অঙ্কিত অভিলম্ব BEB’ কাগজের একই সমতলে অবস্থিত। এটি দ্বারা আলোকের প্রতিসরণের প্রথম সূত্রটি হাইগেনস-এর নীতি অনুসারে (Huygens’s principle) প্রমাণিত হলো।