কৌণিক ভরবেগের নিত্যতা । Conservation of angular momentum
কৌণিক গতির জন্য নিউটনের প্রথম সূত্র হতে আমরা জানি বাহ্যিক টর্কের ক্রিয়াতেই কেবলমাত্র বস্তুর কৌণিক বেগের তথা কৌণিক ভরবেগের পরিবর্তন হয়। টর্কের ক্রিয়া না থাকলে বস্তুটি সমকৌণিক বেগে ঘুরতে থাকে। অর্থাৎ সময়ের সাপেক্ষে কৌণিক বেগ ধ্রুব হয়। ফলে কৌণিক ভরবেগও ধ্রুব হয়। একে কৌণিক ভরবেগের সংরক্ষণ সূত্র (law of Conservation of angular momentum)বলে। সুতরাং বলা যায়, কোনো বস্তুর উপর টর্কের লব্ধি শূন্য হলে বস্তুটির কৌণিক ভরবেগ সংরক্ষিত থাকে।
কৌণিক ভরবেগের সংরক্ষণ সূত্র এর গাণিতিক প্রমাণ ( Mathematical proof of law of Conservation of angular momentum:
আমরা জানি কৌণিক ভরবেগ,
L = I \omega………(4.45)
এখানে L বস্তুর কৌণিক ভরবেগ, I জড়তার ভ্রামক এবং ? কৌণিক বেগ।
সমীকরণ (4.45)-কে সময়ের সাপেক্ষে ব্যবকলন করে পাওয়া যায়,
\frac{dL}{dt} = \frac{d}{dt} (I\omega) = I \frac{d\omega}{dt}কিন্তু \frac{d\omega}{dt} = \alpha
অতএব, \frac{dL}{dt} = I \alpha = \tau [নিউটনের কৌণিক গতি
২য় সূত্র অনুসারে]
এখন, ?=0, অর্থাৎ বস্তুর উপর টর্ক ক্রিয়াশীল না হলে,
\frac{dL}{dt} = 0
∴?= ধ্রুবক
কাজেই, বস্তুর উপর ক্রিয়াশীল টর্কের লব্ধি শূন্য হলে, ঘূর্ণায়মান বস্তুর কৌণিক ভরবেগের পরিবর্তন হবে না। এটিই কৌণিক ভরবেগের সংরক্ষণ সূত্র( law of conservation of angular momentum।
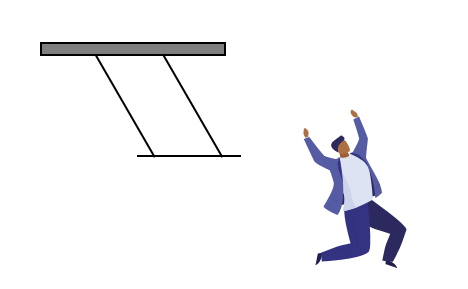
কৌণিক ভরবেগের নিত্যতার চিত্র
উদাহরণ :
তোমরা সার্কাসে ট্রাপিজ খেলা দেখে থাকলে দেখবে খেলোয়াড়রা শূন্যে নানা রকম কসরৎ দেখায়। দোলনা থেকে লাফ দেওয়ার সময় খেলোয়াড়ের হাত ও পা সোজা প্রসারিত থাকে। এই সময় তার কৌণিক বেগ খুব কম থাকে। এবার হাত ও পা গুটিয়ে বুকের কাছে আনলে খেলোয়াড়ের কৌণিক বেগ বেড়ে যায়; ফলে তার পক্ষে শূন্যে পর পর ডিগবাজি খাওয়া সম্ভব হয়। হাত পা গুটিয়ে নেয়ার জন্য খেলোয়াড়টির জড়তের ভ্রামক (?) কমে যায়; কিন্তু তার কৌণিক ভরবেগ ?=?? ধ্রুব থাকে বলে ? কমে যাওয়ায় কৌণিক বেগ ? বেড়ে যায়। [চিত্র]
