যোগজীকরণ, যোগজীকরণ ধ্রুবক, অনির্দিষ্ট যোগজ নির্ণয়ের বিভিন্ন কৌশল, যোগজের যোগশ্রয়ী ধর্ম
যোগজীকরণ (Integration)
প্রতিঅন্তরক হিসেবে যোগজ (Anti-derivative as Integral):
F (x) একটি অন্তরজ F'(x) = f(x) অর্থাৎ \frac{d}{d x}\{F(x)\} হলে, F(x) ফাংশনটিকে f(x) এর প্রতিঅন্তরজ অথবা অনির্দিষ্ট যোগজ (Indefinite Integral) বা সমাকলিত মান বলা হয় এবং ইহাকে \int f(x) d x=F(x) সংকেত দ্বারা নির্দেশ করা হয়। কোনো ফাংশনের যোগজ নির্ণয় করার পদ্ধতিকে যোগজীকরণ (Integration) বলা হয়। এখানে,\int প্রতীক একটি লম্বা S বুঝায়, যাহা ‘Summation’ শব্দটির প্রথম অক্ষর, ফাংশন f(x) কে যোজ্য রাশি (Integrand) বলে এবং অন্তরক dx নির্দেশ করে যে, x যোগজীকরণ চলক। সুতরাং \frac{d}{d x} এবং \int d x পরস্পর বিপরীত প্রক্রিয়া যারা পরস্পর পরস্পরকে প্রশমিত করে।
যোগজীকরণ ধ্রুবক (Constant of Integration):
\frac{d}{d x}\{F(x)\}=f(x) \text { হলে, } \frac{d}{d x}\{F(x)+c\}=\frac{d}{d x}\{F(x)\}+0 \Rightarrow \frac{d}{d x}\{F(x)+c\}=f(x)\Rightarrow F(x)+c=\int f(x) d x
\int f(x) d x=F(x)+c, যেখানে, ‘c’ একটি ইচ্ছাধীন ধ্রুবক যাকে যোগজীকরণ ধ্রুবক বলা হয়। অনির্দিষ্ট যোগজের ক্ষেত্রে যোগজীকরণ ধ্রুবক অবশ্যই লিখতে হবে।
লক্ষণীয়:
- \frac{d}{d x}=D \text { হলে, } D\{F(x)\}=f(x) \Rightarrow D^{-1}\{f(x)\}=F(x)+c
- \frac{d}{d x}\left[\int f(x) d x\right]=\frac{d}{d x}[F(x)+c]=\frac{d}{d x}\{F(x)\}+0=f(x)
- \int\left[\frac{d}{d x}\{f(x)\}\right] d x=\int f(x) d x=F(x)+c
- মনে করি, y=f(x) \therefore \frac{d y}{d x}=f^{\prime}(x) \Rightarrow d y=f^{\prime}(x) d x \Rightarrow d\{f(x)\}=f^{\prime}(x) d x[\because y=f(x)]
উদাহরণস্বরূপ: (\sin x)=\frac{d}{d x}(\sin x) d x=\cos x d x, d\left(3 x^{2}+2 x+5\right)=(6 x+2) d x
অনির্দিষ্ট যোগজ নির্ণয়ের বিভিন্ন কৌশল (Different ways to determine Indefinite Integral):
যোগজীকরণ প্রক্রিয়া অন্তরীকরণ প্রক্রিয়ার বিপরীত এবং এ দুটির মাঝে সম্পর্ক দেখানোর জন্য নিচে কতগুলি ফাংশনের যোগজ ও অন্তরজ দুটিই দেখানো হলো।
- \frac{d}{d x}\left(x^{n}\right)=n x^{n-1} \Rightarrow d\left(x^{n}\right)=n x^{n-1} d x \int x^{n} d x=\frac{x^{n+1}}{n+1}+c,(n \neq-1)
অনু: \text { (a) } \int \frac{1}{x^{n}} d x=\int x^{-n} d x=\frac{x^{-n+1}}{-n+1}+c=\frac{1}{(1-n) x^{n-1}}+c
অনু: \text { (b) } \int d x=\int x^{n} d x=\frac{x^{0+1}}{0+1}+c=x+c
\therefore \int d(\sin x)=\sin x+c, \int d\left(2 x^{3}-3 x\right)=2 x^{3}-3 x+cঅনু: \text { (c) } \int \frac{1}{\sqrt{x}} d x=\int x^{-\frac{1}{2}} d x=\frac{x^{-\frac{1}{2}+1}}{-\frac{1}{2}+1}+c=\frac{x^{\frac{1}{2}}}{\frac{1}{2}}+c=2 \sqrt{x}+c
- d/dx (ln|x|)=1/x⇒d(ln|x|)=1/x dx \int \frac{1}{x} d x=\ln |x|+c, x \neq 0
- \frac{d}{d x}\left(e^{m x}\right)=m e^{m x} \Rightarrow \frac{1}{m} d\left(e^{m x}\right)=e^{m x} d x \int e^{m x} d x=\frac{1}{m} e^{m x}+c, x \neq 0
- \frac{d}{d x}\left(a^{x}\right)=a^{x} \ln a \Rightarrow \frac{1}{\ln a} d\left(a^{x}\right)=a^{x} d x \int a^{x} d x=\frac{a^{x}}{\ln a}+c, a>0, a \neq 1
- \frac{d}{d x}(\sin x)=\cos x \Rightarrow d(\sin x)=\cos x d x \int \cos x d x=\sin x+c
- \frac{d}{d x}(\cos x)=-\sin x \Rightarrow-d(\cos x)=\sin x d x \int \sin x d x=-\cos x+c
- \frac{d}{d x}(\tan x)=\sec ^{2} x \Rightarrow d(\tan x)=\sec ^{2} x d x \int \sec ^{2} x d x=\tan x+c
- \frac{d}{d x}(\cot x)=-\operatorname{cosec}^{2} x \Rightarrow-d(\cot x)=\operatorname{cosec}^{2} x d x \int \operatorname{cosec}^{2} x d x=-\cot x+c
- \cdot \frac{d}{d x}(\operatorname{cosec} x)=-\operatorname{cosec} x \cot x \Rightarrow-d(\operatorname{cosex})=\operatorname{cosec} x \cot x d x \int \operatorname{cosec} x \cot x d x=-\operatorname{cosec} x+c
- \frac{d}{d x}(\sec x)=\sec x \tan x \Rightarrow d(\sec x)=\sec x \tan x d x \int \sec x \tan x d x=\sec x+c
অনুসিদ্ধান্ত:
\frac{d}{d x}\{\sin (a x+b)\}=a \cos (a x+b) \Rightarrow \frac{1}{a} d\{\sin (a x+b)\}=\cos (a x+b) d x
\therefore \int \cos (a x+b) d x=\frac{1}{a} \sin (a x+b)+c \text { অনুরূপভাবে, } \int \sin a x d x=-\frac{1}{a} \cos a x+c,\int \sec ^{2} a x d x=\frac{1}{a} \tan a x+c, \int \operatorname{cosec}^{2} a x d x=-\frac{1}{a} \operatorname{cotax}+c
- \frac{d}{d x}\left(\sin ^{-1} x\right)=\frac{1}{\sqrt{1-x^{2}}} \Rightarrow d\left(\sin ^{-1} x\right)=\frac{1}{\sqrt{1-x^{2}}} d x \quad \int \frac{1}{\sqrt{1-x^{2}}} d x=\sin ^{-1} x+c
- \frac{d}{d x}\left(\tan ^{-1} x\right)=\frac{1}{1+x^{2}} \Rightarrow d\left(\tan ^{-1} x\right)=\frac{1}{1+x^{2}} d x \quad \int \frac{1}{1+x^{2}} d x=\tan ^{-1} x+c
- \frac{d}{d x}\left(\sec ^{-1} x\right)=\frac{1}{x \sqrt{x^{2}-1}} \Rightarrow d\left(\sec ^{-1} x\right)=\frac{1}{x \sqrt{x^{2}-1}} d x \quad \int \frac{1}{x \sqrt{x^{2}-1}} d x=\sec ^{-1} x+c
যোগজের যোগাশ্রয়ী ধর্ম (Linear law of Integrals):
(i) u, v, w, … ইত্যাদি x এর ফাংশন হলে, \int(u+v+w+\cdots) d x=\int u d x+\int v d x+\int w d x+\cdots
প্রমাণ (Proof):
\frac{d}{d x}\left[\int u d x+\int v d x+\int w d x+\cdots\right]=\frac{d}{d x}\left[\int u d x\right]+\frac{d}{d x}\left[\int v d x\right]+\frac{d}{d x}\left[\int w d x\right]+\cdots
\Rightarrow \frac{d}{d x}\left[\int u d x+\int v d x+\int w d x+\cdots\right]=u+v+w+\cdots
অতএব, যোগজের সংজ্ঞা থেকে পাই, \int u d x+\int v d x+\int w d x+\cdots=\int(u+v+w+\cdots) d x
\therefore \int(u+v+w+\cdots) d x=\int u d x+\int v d x+\int w d x+\cdots
(ii) \int c f(x) d x=c \int f(x) d x
প্রমাণ (Proof):
\frac{d}{d x}\left[\int c f(x) d x\right]=c \frac{d}{d x}\left[\int f(x) d x\right] \Rightarrow \frac{d}{d x}\left[\int c f(x) d x\right]=c f(x)
অতএব, যোগজের সংজ্ঞা থেকে পাই, \int c f(x) d x=c \int f(x) d x
নিয়ম-1: যদি কোনো যোজ্য ফাংশনে ???? অথবা ???? বিভিন্ন ঘাত আকারে অথবা ???? ও ???? গুণ আকারে থাকে তবে যোগজীকরণ করবার আগেই তাদের গুণিতক কোণের যোগফল আকারে প্রকাশ করতে হয়। যেমন:-
\sin ^{2} x=\frac{1}{2}(1-\cos 2 x) \quad \cos ^{2} x=\frac{1}{2}(1+\cos 2 x) \sin ^{3} x=\frac{1}{4}(3 \sin x-\sin 3 x) \quad \cos ^{3} x=\frac{1}{4}(3 \cos x+\cos 3 x) \sin A \cos B=\frac{1}{2}[\sin (A+B)+\sin (A-B)] \quad \cos A \sin B=\frac{1}{2}[\sin (A+B)-\sin (A-B)] \cos A \cos B=\frac{1}{2}[\cos (A+B)+\cos (A-B)] \quad \sin A \sin B=\frac{1}{2}[\cos (A-B)-\cos (A+B)]
উদাহরণ-১: নিচের যোগজগুলির মান নির্ণয় কর:
(Example – 1: Determine the following integrals)
(a)\int x(1+\sqrt{x}) d x
(b) \int \frac{d x}{1+\cos x}
(c) \sin ^{-1} \frac{1}{2}
(d) \int 5 \cos 4 x \sin 3 x d x
সমাধান (Solution):
(a) \int x(1+\sqrt{x}) d x=\int\left(x+x^{\frac{3}{2}}\right) d x=\int x d x+\int x^{\frac{3}{2}} d x
=\frac{x^{1+1}}{1+1}+\frac{x^{\frac{3}{2}+1}}{\frac{3}{2}+1}+c
=\frac{x^{2}}{2}+\frac{x^{\frac{5}{2}}}{\frac{5}{2}}+c
=\frac{1}{2} x^{2}+\frac{2}{5} x^{\frac{5}{2}}+c (Ans)
(b) \int \frac{d x}{1+\cos x}=\int \frac{1-\cos x}{(1+\cos x)(1-\cos x)} d x
=\int \frac{1-\cos x}{1-\cos ^{2} x} d x=\int \frac{1-\cos x}{\sin ^{2} x} d x =\int\left[\frac{1}{\sin ^{2} x}-\frac{\cos x}{\sin ^{2} x}\right] d x=\int\left[\operatorname{cosex}^{2}-\operatorname{cosec} x \cdot \cot x\right] d x=-\cot x-(-\operatorname{cosec} x)+c =\operatorname{cosec} x-\cot x+c (Ans)
বিকল্প পদ্ধতিতে সমাধান (Alternative solutions):
\int \frac{d x}{1+\cos x}=\int \frac{d x}{2 \cos ^{2} \frac{x}{2}}
=\frac{1}{2} \int \sec ^{2} \frac{x}{2} d x=\frac{1}{2} \frac{\tan \frac{x}{2}}{\frac{1}{2}}+c=\tan \frac{x}{2}+c (Ans)
\text { (c) } \int \sec ^{2} x \operatorname{cosec}^{2} x d x=\int \frac{1}{\cos ^{2} x \sin ^{2} x} d x =\int \frac{\sin ^{2} x+\cos ^{2} x}{\cos ^{2} x \sin ^{2} x} d x=\int\left[\frac{\sin ^{2} x}{\cos ^{2} x \sin ^{2} x}+\frac{\cos ^{2} x}{\cos ^{2} x \sin ^{2} x}\right] d x =\int\left[\frac{1}{\cos ^{2} x}+\frac{1}{\sin ^{2} x}\right] d x
=\int\left[\sec ^{2} x+\operatorname{cosec}^{2} x\right] d x =\tan x-\cot x+c (Ans)
বিকল্প পদ্ধতি-1 (Alternative way – 1):
\int \sec ^{2} x \operatorname{cosec}^{2} x d x=\int \sec ^{2} x\left(1+\cot ^{2} x\right) d x =\int\left(\sec ^{2} x+\sec ^{2} x \cot ^{2} x\right) d x =\int\left(\sec ^{2} x+\frac{1}{\cos ^{2} x} \times \frac{\cos ^{2} x}{\sin ^{2} x}\right) d x=\int\left(\sec ^{2} x+\operatorname{cosec}^{2} x\right) d x =\tan x-\cot x+c (Ans)
বিকল্প পদ্ধতি-2 (Alternative way – 2):
\int \sec ^{2} x \operatorname{cosec}^{2} x d x=\int \frac{1}{\cos ^{2} x} \cdot \frac{1}{\sin ^{2} x} d x
=\int \frac{4}{(2 \sin x \cos x)^{2}} d x =4 \int \frac{1}{\sin ^{2} 2 x} d x =4 \int \operatorname{cosec}^{2} 2 x d x=4\left(-\frac{1}{2} \cot 2 x\right)+c =-2 \cot 2 x+c (Ans)
(d) \int 5 \cos 4 x \sin 3 x d x=\int \frac{5}{2}[\sin (4 x+3 x)-\sin (4 x-3 x)] d x
=\frac{5}{2} \int(\sin 7 x-\sin x) d x
=\frac{5}{2}\left[-\frac{\cos 7 x}{7}-(-\cos x)\right]+c
=\frac{5}{2}\left(\cos x-\frac{1}{7} \cos 7 x\right)+c (Ans)
অনির্দিষ্ট যোগজ নির্ণয় (Determining Indefinite Integral):
প্রতিস্থাপন পদ্ধতি (Method of substitution):
যোজিত ফল নির্ণয়ে সবচেয়ে প্রয়োজনীয় পদ্ধতি হচ্ছে প্রতিস্থাপন পদ্ধতি। প্রদত্ত যোজ্য রাশির অন্তর্ভুক্ত কোনো ফাংশনের পরিবর্তে একটি চলরাশি স্থাপন করে যোজিত ফল নির্ণয়ের পদ্ধতিকে প্রতিস্থাপন বলা হয়।
উপপাদ্য: x=g(z) \text {হলে, } \int f(x) d x=\int f\{g(z)\} g^{\prime}(z) d z
(Theorem: If x=g(z) \text {হলে, } \int f(x) d x=\int f\{g(z)\} g^{\prime}(z) d z)
প্রমাণ (Theorem proof):
মনে করি, F(x)=\int f(x) d x \Rightarrow \frac{d}{d x}\{F(x)\}=f(x)
x=g(z) \text { বলে, } \frac{d x}{d z}=g^{\prime}(z) \ldots \ldots(2)
এখন, \text { এथन, } \frac{d}{d z}\{F(x)\}=\frac{d}{d x}\{F(x)\} \cdot \frac{d x}{d z}=f(x) \cdot g^{\prime}(z) [(1) ও (2) হতে]
\frac{d}{d z}\{F(x)\}=f\{g(z)\} \cdot g^{\prime}(z)[\because x=g(z)] (x)=\int f\{g(z)\} \cdot g^{\prime}(z) d z \Rightarrow \int f(x) d x=\int f\{g(z)\} \cdot g^{\prime}(z) d z
দ্রষ্টব্য (Note): (2) থেকে পাই, d x=g^{\prime}(z) d z \Rightarrow d\{g(z)\}=g^{\prime}(z) d z
\int f(x) d x=\int f\{g(z)\} \cdot g^{\prime}(z) d z=\int f\{g(z)\} d\{g(z)\}
ধরন-১ (Type – 1): যোজ্য রাশি f(x)=g(x) \times g^{\prime}(x) \text { বা, }\{g(x)\}^{n} \times g^{\prime}(x) \text { বা, } T\{g(x)\} . g^{\prime}(x)
এখানে, T=\sin , \cos , \sec ^{2} \ldots \text { বা, }[T\{g(x)\}]^{n} \times g^{\prime}(x) \text {বা, } e^{T\{g(x)\}} \cdot g^{\prime}(x) ইত্যাদি আকারে থাকে।
অর্থাৎ যদি যোজ্য রাশি f(x) এর এক অংশ g(x) কে অন্তরীকরণ করলে অপর অংশ পাওয়া যায়, তবে g(x) = z ধরে রাশিটির যোজিত ফল নির্ণয় করা যায়।
উদাহরণ-২: নিচের যোগজগুলির মান নির্ণয় কর:
(Example – 2: Determine the following integrals)
(a) <span style="font-weight: 400;">\int(3-2 x)^{4} d x</span>
(b) \int \cos x e^{\sin x} d x
সমাধান (Solution):
(a) মনে করি, 3-2 x=z \therefore-2 d x=d z \Rightarrow d x=-\frac{1}{2} d z
∴\int(3-2 x)^{4} d x=\int z^{4}\left(-\frac{1}{2} d z\right)
=-\frac{1}{2} \cdot \frac{z^{4+1}}{4+1}+c
=-\frac{1}{10}(3-2 x)^{5}+c (Ans)
বিকল্প পদ্ধতিতে সমাধান (Alternative solutions):
\int(3-2 x)^{4} d x
=-\frac{1}{2} \int(3-2 x)^{4}(-2 d x), \quad[\because d(3-2 x)=-2 d x] =-\frac{1}{2} \cdot \frac{(3-2 x)^{4+1}}{4+1}+c
=-\frac{1}{10}(3-2 x)^{5}+c (Ans)
(b) মনে করি, \sin x=z \therefore \cos x d x=d z
\therefore \int \cos x e^{\sin x} d x=\int e^{\sin x} \cos x d x
=\int e^{z} d z=e^{z}+c=e^{\sin x}+c \quad[\because d(\sin x)=\cos x d x] (Ans)
বিকল্প পদ্ধতিতে সমাধান (Alternative solutions):
\int \cos x e^{\sin x} d x
=\int e^{\sin x}(\cos x d x)
=e^{\sin x}+c \quad[\because d(\sin x)=\cos x d x] (Ans)
ধরন-২ (Type – 2):
(a) \int \frac{f^{\prime}(x)}{f(x)} d x=\int \frac{d\{f(x)\}}{f(x)}=\ln |f(x)|+c
(b) \int \frac{f^{\prime}(x)}{\sqrt{f(x)}} d x=\int \frac{d\{f(x)\}}{\sqrt{f(x)}}=2 \sqrt{f(x)}+c
নিয়ম (Rule): f (x) = z ধরতে হয়।
প্রমাণ (Proof):
মনে করি, f(x)=z \quad \therefore f^{\prime}(x) d x=d z
\therefore \int \frac{f^{\prime}(x)}{f(x)} d x=\int \frac{d z}{z}=\ln |z|+c
এবং \int \frac{f^{\prime}(x)}{\sqrt{f(x)}} d x=\int \frac{d z}{\sqrt{z}}=2 \sqrt{z}+c=2 \sqrt{f(x)}+c
উদাহরণ-৩: নিচের যোগজগুলির মান নির্ণয় কর।
(Example – 3: Determine the following integrals)
(a) \int \tan x d x
(b) \int \sec x d x
(c) \int \operatorname{cosec} x d x
সমাধান (Solution):
(a) \int \tan x d x=\int \frac{-(-\sin x d x)}{\cos x}
=-ln|cosx|+c
=\ln |\sec x|+c (Ans)
(b) \int \sec x d x
=\int \frac{\sec x(\sec x+\tan x)}{(\sec x+\tan x)} d x
=\int \frac{\sec x \tan x+\sec ^{2} x}{(\sec x+\tan x)} d x
=\ln |\sec x+\tan x|+c (Ans)
(c) \int \operatorname{cosec} x d x
=\int \frac{d x}{\sin x}=\int \frac{d x}{2 \sin \frac{x}{2} \cos \frac{x}{2}} =\int \frac{\sec ^{2} \frac{x}{2} d x}{\sec ^{2} \frac{x}{2} \cdot 2 \sin \frac{x}{2} \cos \frac{x}{2}} =\int \frac{\left(\frac{1}{2} \sec ^{2} \frac{x}{2}\right) d x}{\tan \frac{x}{2}}
=-\ln \left|\tan \frac{x}{2}\right|+c (Ans)
উদাহরণ-৪: নিচের যোগজগুলির মান নির্ণয় কর।
(Example 4 – Determine the following integrals)
(a) \int \frac{1+\cos x}{x+\sin x} d x
(b) \int \frac{\tan x}{\ln \cos x} d x
সমাধান (Solution):
(a) মনে করি, x+\sin x=z \quad \therefore(1+\cos x) d x=d z
∴\therefore \int \frac{1+\cos x}{x+\sin x} d x=\int \frac{d z}{z}
=\ln |z|+c
=\ln |x+\sin x|+c (Ans)
বিকল্প পদ্ধতিতে সমাধান (Alternative solutions):
\int \frac{1+\cos x}{x+\sin x} d x=\int \frac{d(x+\sin x)}{x+\sin x} d x
= ln|x+sinx|+c (Ans)
(b) মনে করি, \ln \cos x=z \quad \therefore \frac{-\sin x}{\cos x} d x=d z \Rightarrow \tan x d x=-d z
=\int \frac{\tan x}{\ln \cos x} d x=-\int \frac{d z}{z} =-\ln z+c
=-\ln (\ln \cos x)+c (Ans)
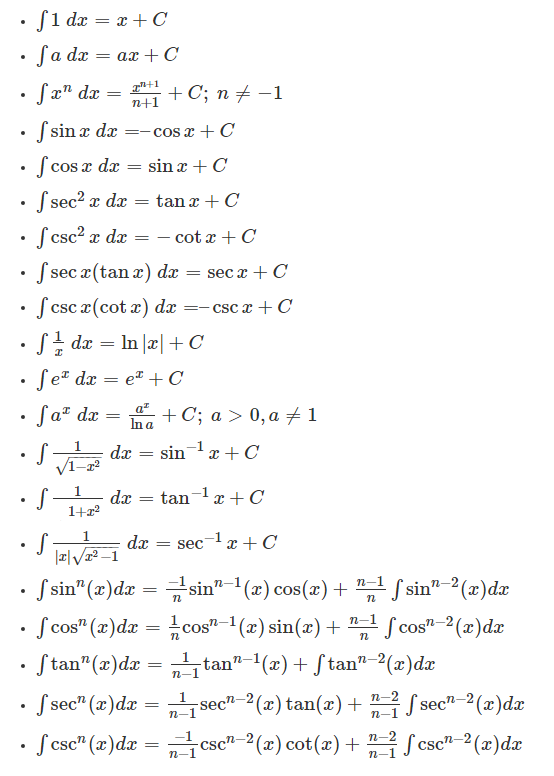
Integration Formulas
এইচএসসি ও এডমিশন পরীক্ষার্থীদের জন্য আমাদের কোর্সসমূহঃ
- HSC 25 অনলাইন ব্যাচ ২.০ (বাংলা, ইংরেজি, তথ্য ও যোগাযোগ প্রযুক্তি)
- HSC 26 অনলাইন ব্যাচ (বাংলা, ইংরেজি, তথ্য ও যোগাযোগ প্রযুক্তি)
- HSC 25 অনলাইন ব্যাচ (ফিজিক্স, কেমিস্ট্রি, ম্যাথ, বায়োলজি)
- HSC 26 অনলাইন ব্যাচ (ফিজিক্স, কেমিস্ট্রি, ম্যাথ, বায়োলজি)
- মেডিকেল এডমিশন কোর্স – ২০২৪
- ঢাকা ভার্সিটি A Unit এডমিশন কোর্স – ২০২৪
- ঢাকা ভার্সিটি B Unit এডমিশন কোর্স – ২০২৪
- বুয়েট কোশ্চেন সলভ কোর্স
- গুচ্ছ A Unit এডমিশন কোর্স – ২০২৪
- গুচ্ছ B Unit এডমিশন কোর্স – ২০২৪
আমাদের স্কিল ডেভেলপমেন্ট কোর্সসমূহঃ
- বিদেশে উচ্চশিক্ষা: Study Abroad Complete Guideline
- Student Hacks
- IELTS Course by Munzereen Shahid
- Complete English Grammar Course
- Microsoft Office 3 in 1 Bundle
- ঘরে বসে Freelancing
- Facebook Marketing
- Adobe 4 in 1 Bundle
১০ মিনিট স্কুলের ক্লাসগুলো অনুসরণ করতে ভিজিট: www.10minuteschool.com
