গড় মুক্ত পথ বা গড় নির্বাধ দূরত্ব এবং স্বাধীনতার মাত্রা (Mean Free Path And Degrees of Freedom)

গড় মুক্ত পথ বা গড় নির্বাধ দূরত্ব (Mean Free Path)

সংজ্ঞা: কোনো অণুর পরপর দুটি সংঘর্ষের মধ্যবর্তী দূরত্বগুলোর গড় নিলে যে দূরত্ব পাওয়া যায় তাকেই গড় মুক্ত পথ (Mean Free Path) বলে।

যদি N সংখ্যক ধাক্কার ভেতর অণু মোট l দূরত্ব অতিক্রম করে তবে গড় মুক্ত পথ, \lambda=\frac{l}{N}।

ধরা যাক, কোনো গ্যাসের প্রতি একক আয়তনে অণুর সংখ্যা n এবং প্রতিটি অণুর ব্যাস \sigma। আমরা যে অণুটির গড় মুক্ত পথ নির্ণয় করছি হিসাবের সুবিধার জন্য কেবলমাত্র সে অণুটিকে গতিশীল ধরে বাকি অণুগুলোকে স্থির বিবেচনা করছি।

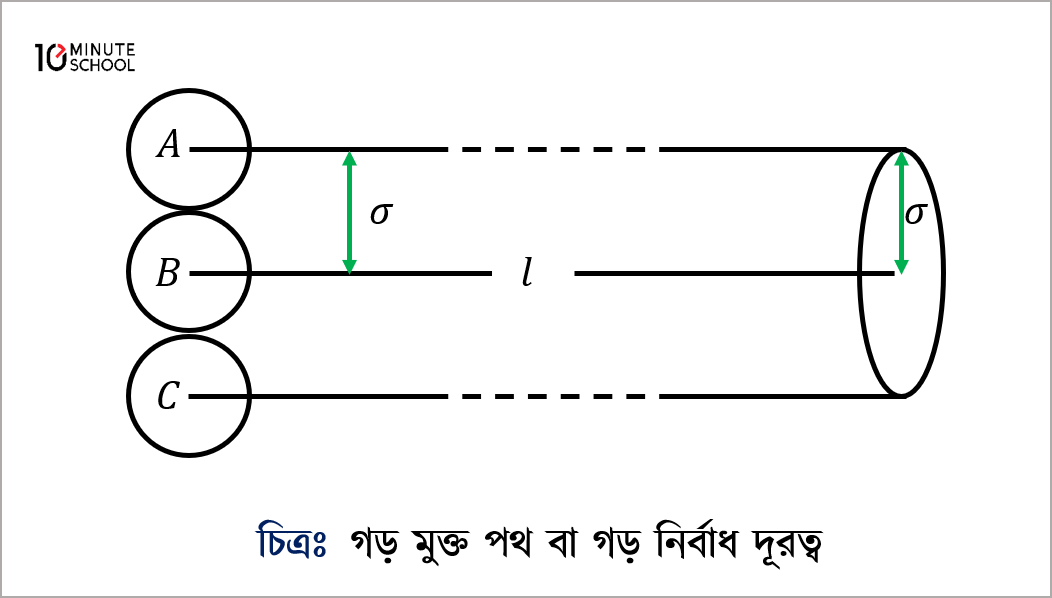
(১০.১০) চিত্রে আমরা C অণুটির গড় মুক্ত পথ হিসাব করতে চাই। C অণুটি l দূরত্ব অতিক্রম করার সময় অন্য যে সকল অণুর কেন্দ্র C অণুটির কেন্দ্র থেকে \sigma  দূরে, (চিত্রে A ও B অণুদ্বয়) অথবা \sigma  অপেক্ষা কম দূরে থাকবে তাদের সাথে ধাক্কা খাবে। অর্থাৎ \sigma  ব্যাসার্ধ ও l  দৈর্ঘ্যের একটি সিলিন্ডারের মধ্যে যে সকল অণুর কেন্দ্র থাকবে C অণুটি কেবলমাত্র তাদের সাথে ধাক্কা খাবে। এ সিলিন্ডারের আয়তন \pi \sigma^{2} l। এখন একক আয়তনে অণুর সংখ্যা n হলে \pi \sigma^{2} l আয়তনে মোট অণুর সংখ্যা হবে n \pi \sigma^{2} ll অর্থাৎ l দূরত্ব অতিক্রম করার সময় C অণুটি n \pi \sigma^{2} ll সংখ্যক বার ধাক্কা খাবে।

যেহেতু কোনো অণুর পর পর দুটি সংঘর্ষের মধ্যবর্তী দূরত্বগুলোর গড় নিলে যে দূরত্ব পাওয়া যায় তাকে গড় মুক্ত পথ বলে।

অতএব গড় মুক্ত পথ, \lambda=\frac{\text { অতিত্রান্ত দূরত্ব }}{\text { ধাক্কা সংখ্যা }}=\frac{l}{n \pi \sigma^{2} l}

\therefore \lambda=\frac{1}{n \pi \sigma^{2}} …   …   …   …  (10.28)

গড় মুক্ত পথের সাথে আণবিক ব্যাস \sigma , ও একক আয়তনে গ্যাসের অণুর সংখ্যা n–এর উপরিউক্ত সম্পর্ক নির্ণয় করেন ক্লাসিয়াস।

ধরা যাক, একটি অণুর ভর =m। যেহেতু একক আয়তনে অণুর সংখ্যা n, কাজেই একক আয়তনে অণুর ভর =mn= গ্যাসের ঘনত্ব । (10.28) সমীকরণের হর ও লবকে m দিয়ে গুণ করে আমরা পাই,

\lambda=\frac{m}{\pi \sigma^{2} m n}=\frac{m}{\pi \sigma^{2} \rho}

বা, \lambda \propto \frac{1}{\rho} \quad   [এখানে K একটি ধ্রুবক]

সুতরাং গড় মুক্ত পথ গ্যাসের ঘনত্বের ব্যস্তানুপাতিক। কিন্তু গ্যাসের ঘনত্ব, গ্যাসের চাপের সমানুপাতিক এবং পরম তাপমাত্রার ব্যস্তানুপাতিক। কাজেই গড় মুক্ত পথ গ্যাসের চাপের ব্যস্তানুপাতিক এবং পরম তাপমাত্রার সমানুপাতিক।

গড় মুক্ত পথের অন্যান্য রাশিমালা (Other equations of mean free path)

ক্লাসিয়াসের পদ্ধতিতে গড় মুক্ত পথ গণনা নির্ভুল নয়। কারণ, যে অণুর গড় মুক্ত পথ নির্ণয় করা হয়েছে সেটি ছাড়া অন্য অণুগুলোকে স্থির ধরা হয়েছে। কিন্তু প্রকৃতপক্ষে সকল অণুই গতিশীল। বোল্‌জম্যান সকল অণুর গড়বেগ সমান ধরে গড় মুক্ত পথের রাশিমালা নির্ণয় করেন,

\lambda=\frac{3}{4 \pi \sigma^{2} n} …   …   …   …  (10.29)

পরে ম্যাক্সওয়েল তাঁর বেগ বণ্টনের সূত্রের সাহায্যে গড় মুক্ত পথের রাশিমালা নির্ণয় করেন,

\lambda=\frac{1}{\sqrt{2} \pi \sigma^{2} n} …   …   …   …  (10.30)

গড় মুক্তপথ নির্ণয়ের জন্যে \lambda=\frac{1}{\sqrt{2} \pi \sigma^{2} n} সমীকরণটি ব্যবহার করা হয়ে থাকে।

গড় মুক্ত পথ সংক্রান্ত ক্লাসিয়াস ও বোলজম্যানের ও ম্যাক্সওয়েলের সমীকরণ তুলনা কর।

গড় মুক্তপথের ক্লাসিয়াসের সমীকরণ হচ্ছে–

\lambda_{C}=\frac{1}{n \pi \sigma^{2}} …   …   …   …  (10.31)

এবং বোলজম্যানের সমীকরণ হচ্ছে, 

\lambda_{B}=\frac{3}{4 n \pi \sigma^{2}} …   …   …   …  (10.32)

এবং গড় মুক্তপথের ম্যাক্সওয়েলের সমীকরণ হচ্ছে,  

\begin{aligned} \lambda_{M} &=\frac{1}{\sqrt{2} n \pi \sigma^{2}} \\ ...   ...   ...   ...  (10.33) \therefore \frac{\lambda_{C}}{\lambda_{B}} &=\frac{1}{n \pi \sigma^{2}} \div \frac{3}{4 n \pi \sigma^{2}}=\frac{4}{3} \end{aligned}\\ \lambda_{C}: \lambda_{B}=4: 3 \\ \quad \frac{\lambda_{C}}{\lambda_{M}}=\frac{1}{n \pi \sigma^{2}} \div \frac{1}{\sqrt{2} n \pi \sigma^{2}}=\sqrt{2}\\ \lambda_{C}: \lambda_{M}=\sqrt{2}: 1

স্বাধীনতার মাত্রা (Degrees of Freedom)

সংজ্ঞা: কোনো গতিশীল সিস্টেমের অবস্থান সম্পূর্ণভাবে বোঝাতে মোট যে সংখ্যক স্বাধীন রাশির প্রয়োজন হয় তাকে বা গতিশীল সিস্টেমের মোট গতিশক্তির রাশিমালায় যে কয়টি স্বাধীন বর্গ রাশি পাওয়া যায় সেই সংখ্যাকে স্বাধীনতার মাত্রার সংখ্যা বলে।

কোনো গতিশীল সিস্টেমের অবস্থান সম্পূর্ণরূপে প্রকাশ করতে যতগুলো স্থানাঙ্কের প্রয়োজন হয় তার সংখ্যাই হচ্ছে স্বাধীনতার মাত্রা।

কোনো সিস্টেমের স্বাধীনতার মাত্রার সংখ্যা = সিস্টেমের উপাদানগুলোর অবস্থান সম্পূর্ণরূপে প্রকাশ করতে প্রয়োজনীয় মোট স্থানাঙ্কের সংখ্যা এবং উপাদানগুলোর পরস্পরের ভিতর স্বতন্ত্রভাবে যে সম্পর্ক রয়েছে তার অন্তর ফলের সমান। 

কোনো গ্যাস অণুতে x সংখ্যক পরমাণু থাকলে স্বাধীনতার মাত্রা সর্বাধিক হবে 3x। এখন এক পরমাণু গ্যাসের বেলায় x=1, কাজেই এক্ষেত্রে স্বাধীনতার মাত্রা হবে 3। দ্বি-পারমাণবিক গ্যাসের বেলায় x=2, কাজেই স্বাধীনতার মাত্রা হওয়া উচিত 3×2=6। কিন্তু পরমাণু দুটি পরস্পরের মধ্যে নির্দিষ্ট দূরত্ব বজায় রাখায় অর্থাৎ পরমাণু দুটির মধ্যে একটি সম্পর্ক থাকায় স্বাধীনতার মাত্রা হবে 3×2-1=5। বহু পারমাণবিক যেমন ত্রি-পারমাণবিক গ্যাসের ক্ষেত্রে পরমাণু তিনটি, অণুর ভিতরে দুভাবে সজ্জিত থাকতে পারে। যেমন মাঝখানে একটি এবং দুপাশে দুটি বা ত্রিভুজের তিন কোণে তিনটি। প্রথম ক্ষেত্রে স্বাধীনতার মাত্রা হবে 3×3-2=7 এবং দ্বিতীয় ক্ষেত্রে হবে 3×3-3=6।