ফাংশনের জন্য লিমিট এর মান নির্ণয় (Determining the value of the limit for different functions)

Type 04- ত্রিকোণমিতি ফাংশনের লিমিট (Limit of trigonometry function):

Q. $\frac{\lim }{x \rightarrow 0} \frac{1-\cos 7 x}{3 x^{2}}$

\begin{array}{l} =\frac{\lim }{x \rightarrow 0} \frac{2 \sin ^{2} \frac{7 x}{2}}{3 x^{2}} \\ =\frac{2}{3} \frac{\lim }{x \rightarrow 0}\left(\frac{\sin \frac{7 x}{2}}{\frac{7 x}{2}}\right)^{2} \times\left(\frac{7 x}{2}\right)^{2} \times \frac{1}{x^{2}} \\ =\frac{2}{3} \times \frac{7^{2}}{4}=\frac{49}{6} \end{array}

(Ans)

Q. $\frac{\lim }{x \rightarrow 0} \frac{\tan x-\sin x}{x^{3}}$

\begin{array}{l} =\frac{\lim }{x \rightarrow 0} \frac{\tan x(1-\cos x)}{x^{3}} \\ =\frac{\lim }{x \rightarrow 0} \frac{\tan x \times 2 \sin ^{2} \frac{x}{2}}{x^{3}} \\ =\frac{\lim }{x \rightarrow 0} \frac{\tan x}{x} \\ =\frac{\lim }{x \rightarrow 0} \frac{\sin x}{x} \frac{x}{2} \\ =2 \times \frac{1}{4}=\frac{1}{2} \\ \end{array}

(Ans)

Example-27: $\frac{\lim }{x \rightarrow 0} \frac{\cos 7 x-\cos 9 x}{\cos 3 x-\cos 5 x}$

Sol $^{n}: \frac{\lim }{x \rightarrow 0} \frac{\cos 7 x-\cos 9 x}{\cos 3 x-\cos 5 x}$

\begin{array}{l} =\frac{\lim }{x \rightarrow 0} \frac{\cos 7 x-\cos 9 x}{\cos 3 x-\cos 5 x} \\ =\frac{\frac{\lim }{x \rightarrow 0} \frac{\sin 8 x}{8 x} \cdot 8 x}{\frac{\lim \sin 4 x}{x \rightarrow 0} 4 x} \cdot 4 x \\ =2 \end{array}

(Ans)

Type-05: $x$ এর মান অসীমের দিকে ধাবিত হলে লিমিটের মান নির্ণয় (Determining the value of limit if the value of $x$ runs towards infinity) :

Example-13: $\frac{L t}{x \rightarrow \infty} \frac{a x^{2}+b x+c}{L x^{2}+m x+n}$ এর মান কত?

$\mathrm{Sol}^{n}$ : $\frac{L t}{x \rightarrow \infty} \frac{\left(a+\frac{b}{x}+\frac{c}{x^{2}}\right)}{\left(l+\frac{m}{x}+\frac{n}{x^{2}}\right)}$ = $\frac{a+0+0}{l+0+0}$ = $x$

(Ans)

Example-14: $\frac{\lim }{x \rightarrow \infty} \frac{1^{2}+2^{2}+3^{2}+----+x^{2}}{x^{3}+x^{2}+x+1}$ এর মান কত?

$\mathrm{Sol}^{n}$ : $\frac{\lim }{x \rightarrow \infty} \frac{1^{2}+2^{2}+3^{2}+----+x^{2}}{x^{3}+x^{2}+x+1}$

= $\frac{\lim }{x \rightarrow \infty} \frac{x(x+1)(2 x+1)}{6\left(x^{3}+x^{2}+x+1\right)}$

= $\frac{\lim }{x \rightarrow \infty} \frac{2 x^{3}+2 x^{2}+x}{6 x^{3}+6 x^{2}+6 x+6}$

= $\frac{\lim }{x \rightarrow \infty} \frac{2+\frac{3}{x}+\frac{1}{x^{2}}}{6+\frac{6}{x}+\frac{6}{x^{2}}+6 / x^{3}}$

= $\frac{2+0+0}{6+0+0+0}$ = $\frac{2}{6}$ = $\frac{1}{3}$

(Ans)

Q. $\frac{\lim }{x \rightarrow \infty} \frac{3^{x}-3^{-x}}{3^{x}+3^{-x}}$

$\begin{array}{l} =\frac{\lim }{x \rightarrow \infty} \frac{3^{x}\left(1-3^{-2 x}\right)}{3^{x}\left(1+3^{-2 x}\right)} \\ =\frac{\lim }{x \rightarrow \infty} \frac{1-\frac{1}{3^{2 x}}}{1-\frac{1}{3^{2 x}}} \\ =1 \\ \end{array}$

(Ans)

\begin{array}{l} \text { Q. } \frac{\lim }{n \rightarrow \infty} \frac{1}{n^{4}} \sum_{r=1}^{n} \boldsymbol{r}^{3} \\ =\frac{\lim }{n \rightarrow \infty} \frac{1}{n^{4}}\left\{1+2^{3}+3^{3}+----n^{3}\right\} \\ =\frac{\lim }{n \rightarrow \infty} \frac{1}{n^{4}}\left\{\frac{n(n+1)}{2}\right\}^{2} \\ =\frac{\lim }{n \rightarrow \infty} \frac{1}{n^{4}}\left\{\frac{n^{2}\left(1+\frac{1}{n}\right)^{2}}{4}\right\} \\ =\frac{1}{4} \cdot \frac{\lim }{n \rightarrow \infty} \frac{1}{n^{2}}\left(1+\frac{1}{n}\right)^{2} \\ =\frac{1}{4} \cdot 1=\frac{1}{4} \\ \end{array}

(Ans)

Type-05: Inverse circular function এর লিমিট নির্ণয় (Determine the limit of inverse circular function) :

Concept: (i) Inverse circular functiom থাকবে ; (ii) বীজগাণিতিক বা ত্রিকোণ্মিতিক ফাংশন ; (iii) limx→0 থাকবে।

Example- 39. মান নির্ণয় করঃ $\frac{L t}{x \rightarrow 0} \frac{\tan ^{-1} x}{x}$

Sol $^{n}$ : ধরি, $\tan ^{-1} x=\theta$ বা $\tan \theta=x$ যেহেতু $x \rightarrow 0$ তাই $\theta \rightarrow 0$

\therefore \frac{L t}{x \rightarrow 0} \frac{\tan ^{-1} x}{x}=\frac{L t}{\theta \rightarrow 0} \frac{\theta}{\tan \theta}=\frac{L t}{\theta \rightarrow 0} \frac{\frac{1}{\tan \theta}}{\theta}=1

(Ans)

⟹ ফাংশনের অন্তরীকরণ যোগ্যতাঃ

একটি ফাংশন তখনি অন্তরীকরণ যোগ্য হবে যখন ফাংশনটি অবিচ্ছিন্ন হবে। বিচ্ছিন্ন ফাংশনের অন্তরীকরণ সম্ভব নয়।

⟹ প্রায়োগিক ভাষায় অন্তরীকরণ একটি রৈখিক প্রক্রিয়া যা ইনপুট করে একটি ফাংশন এবং আউটপুট করে অপর একটি ফাংশন এরূপ যেন, প্রতিটি বিন্দুতে আউটপুটের মান হয় ইনপুট ঢাল।

ফাংশন

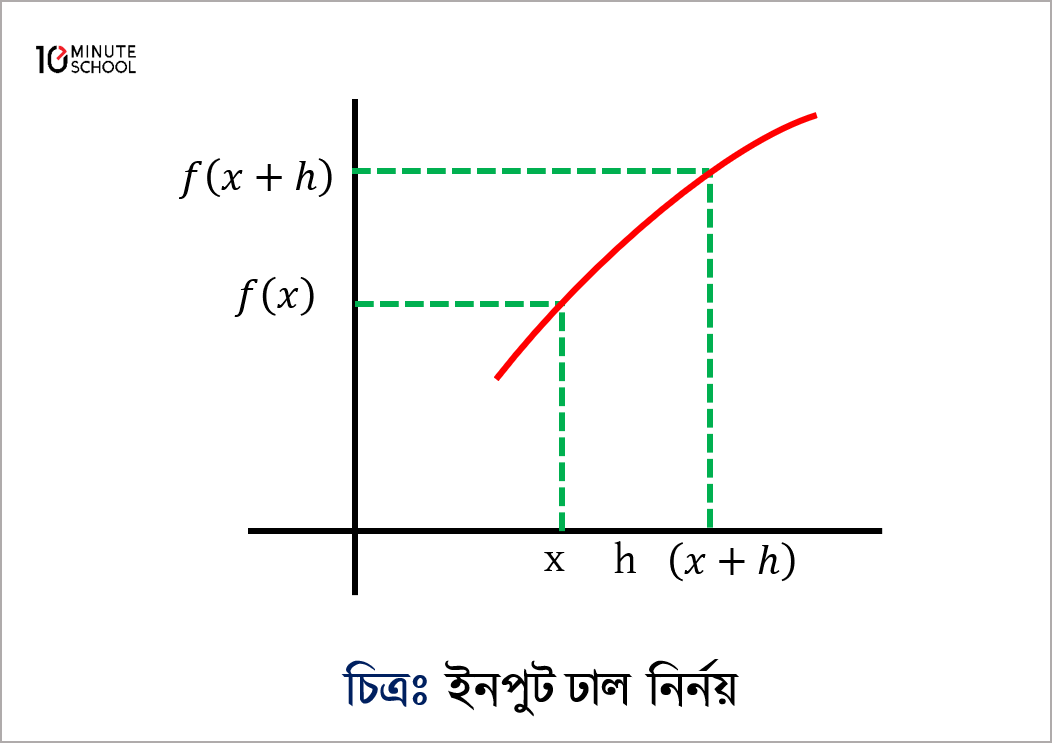
∴ ঢাল = $\frac{\Delta y}{\Delta x}$ = $\frac{f(x+h)-f(x)}{x+h-x}$ = $\frac{f(x+h)-f(x)}{h}$

যখন $x$ এর পরিবর্তন অতিক্ষুদ্র অর্থাৎ $h\to0$ তখন $x$ এর সাপেক্ষে $y$ এর যে পরিবর্তন হয় তাকে $y$ এর অন্তরজ বলে।

অর্থাৎ,

$\frac{\lim }{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}$ ⟶ মূল নিয়মে অন্তরজ সূত্র।

$\frac{\lim }{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}$ = $\frac{d y}{d x}$

$\frac{d y}{d x}$ = ঢাল = $m$ = $\tan \theta$ = $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ = $\frac{\Delta y}{\Delta x}$ = $f^{\prime}(x)=y_{1}$

মূলনিয়মের অন্তরীকরণঃ

(i) $\frac{d}{d x}^{(\sin x)}$ নির্ণয়ঃ

\begin{array}{l} \frac{d}{d x}^{(\sin x)}=\frac{\lim }{h \rightarrow 0} \frac{\sin (x+h)-\sin x}{h} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times 2 \cos \frac{x+h+x}{2} \cdot \sin \frac{x+h-x}{2} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times 2 \cos \frac{2 x+h}{2} \cdot \sin \frac{h}{2} \\ =2 \times \frac{\lim }{\frac{h}{2} \rightarrow 0} \frac{\sin \frac{h}{2}}{\frac{h}{2}} \times \frac{h}{2} \times \frac{\lim }{h \rightarrow 0} \cos \frac{2 x+h}{2} \times \frac{1}{h} \\ =2 \times \frac{\lim }{h \rightarrow 0} \frac{h}{2} \times \frac{1}{h} \times \cos \frac{2 x+h}{2} \\ =\cos \frac{2 x}{2}=\cos x \\ \therefore \frac{d}{d x}(\sin x)=\cos x \end{array}

(ii) $\frac{d}{d x}^{(\cos x)}$ নির্ণয়ঃ

\begin{array}{l} \frac{d}{d x}^{(\cos x)}=\frac{\lim }{h \rightarrow 0} \frac{\cos (x+h)-\cos x}{h} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times 2 \sin \frac{x+h+x}{2} \cdot \sin \frac{x-h-x}{2} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times 2 \sin \frac{2 x+h}{2} \cdot \sin \frac{-h}{2} \\ =-2 \times \frac{\lim }{\frac{h}{2} \rightarrow 0} \frac{\sin \frac{h}{2}}{\frac{h}{2}} \times \frac{\lim }{h \rightarrow 0} \frac{1}{h} \times \frac{h}{2} \sin \frac{2 x+h}{2} \\ =-2 \times \frac{1}{2} \sin \frac{2 x}{2}=-\sin x \\ \therefore \frac{d}{d x}^{(\cos x)}=-\sin x \end{array}

(iii) $\frac{d}{d x}^{(\tan x)}$ নির্ণয়ঃ

$\begin{array}{l} \frac{d}{d x}^{(\tan x)}=\frac{\lim }{h \rightarrow 0} \frac{\tan (x+h)-\tan x}{h} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times\left(\frac{\sin (x+h)}{\cos (x+h)}-\frac{\sin x}{\cos x}\right) \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times \frac{\sin (x+h) \cdot \cos x-\sin x \cdot \cos (x+h)}{\cos (x+h) \cdot \cos x} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h \cos (x+h) \cdot \cos x} \times \sin (x+h-x) \\ =\frac{\lim }{h \rightarrow 0} \frac{\sin h}{h} \times \frac{1}{\cos (x+h) \cdot \cos x} \\ =\frac{1}{\cos ^{2} x}=\sec ^{2} x \\ \therefore \frac{d}{d x}(\tan x) \end{array}$

(iv) $\frac{d}{d x}^{(\cot x)}$ নির্ণয়ঃ

$\begin{array}{l} \frac{d}{d x}^{(\cot x)} \quad=\frac{\lim }{h \rightarrow 0} \frac{\cot (x+h)-\cot x}{h} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times\left(\frac{\cos (x+h)}{\sin (x+h)}-\frac{\cos x}{\sin x}\right) \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times\left(\frac{\cos (x+h) \cdot \sin x-\cos x \cdot \sin (x+h)}{\sin (x+h) \cdot \sin x}\right) \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times \frac{\sin (x-x-h)}{\sin (x+h) \cdot \sin x} \\ =\frac{\lim }{h \rightarrow 0} \times \frac{-\sin h}{h \sin (x+h) \cdot \sin x} \\ =-\frac{\lim }{h \rightarrow 0} \frac{\sin h}{h} \times \frac{\lim }{h \rightarrow 0} \frac{h}{\operatorname{hsin}(x+h) \cdot \sin x} \\ =-\frac{1}{\sin ^{2} x}=-\operatorname{cosec}^{2} x \\ \therefore \frac{d}{d x}(\cot x) \\ \end{array}$

(v) $\frac{d}{d x}^{(\sec x)}$ নির্ণয়ঃ

$\begin{array}{l} \frac{d}{d x}^{(\sec x)}=\frac{\lim }{h \rightarrow 0} \frac{\sec (x+h)-\sec x}{h} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times\left(\frac{1}{\cos (x+h)}-\frac{1}{\cos x}\right) \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times \frac{\cos x-\cos (x+h)}{\cos (x+h) \cdot \cos x} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{\cos (x+h) \cdot \cos x} \cdot 2 \sin \frac{2 x+h}{2} \cdot \frac{\lim }{h \rightarrow 0} \cdot \sin \frac{x+h-x}{2} \\ =\frac{\lim }{h \rightarrow 0} \frac{\sin \frac{h}{2}}{\frac{h}{2}} \times \frac{\lim }{h \rightarrow 0} \frac{2 \sin \left(x+\frac{h}{2}\right)}{\cos (x+h) \cdot \cos x} \cdot \times \frac{2}{2} \\ =\frac{1}{\cos ^{2} x} \cdot \sin \frac{2 x}{2} \\ =\frac{\sin x}{\cos x} \times \frac{1}{\cos x} \\ =\tan x \cdot \sec x \\ \therefore \frac{d}{d x}(\sec x) \end{array}$

(vi) $\frac{d}{d x}^{(\operatorname{cosec} x)}$ নির্ণয়ঃ

$\begin{array}{l} \frac{d}{d x}^{(\operatorname{cosec} x)}=\frac{\lim }{h \rightarrow 0} \frac{\operatorname{cosec}(x+h)-\operatorname{cosec} x}{h} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times\left(\frac{1}{\sin (x+h)}-\frac{1}{\sin x}\right) \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times \frac{\sin x-\sin (x+h)}{\sin (x+h) \sin x} \\ =\frac{\lim }{h \rightarrow 0} \times \frac{1}{h \sin (x+h) \sin x} \times 2 \cos \frac{x+x+h}{2} \cdot \sin \frac{x-x-h}{2} \\ =\frac{\lim }{h \rightarrow 0} \times \frac{1}{h \sin (x+h) \sin x} \times 2 \cos \frac{2 x+h}{2}-\sin \frac{h}{2} \\ =\frac{\lim }{h \rightarrow 0} \frac{\sin \frac{h}{2}}{h} \times \frac{\lim }{h \rightarrow 0} \frac{h}{2} \times \frac{2 \cos \frac{2 x+h}{2}}{h \sin (h+x) \cdot \sin x} \\ =-\frac{\cos \frac{2 x}{2}}{\sin ^{2} x}=-\frac{\cos x}{\sin x} \times \frac{1}{\sin x} \\ =-\cot x . \operatorname{cosec} x \\ \therefore \frac{(\operatorname{cosec} x)}{d x} \end{array}$

(vii) $\frac{d}{d x}^{e^{x}}$ নির্ণয়ঃ

$\begin{array}{l} \frac{d e^{x}}{d x}=\frac{\lim }{h \rightarrow 0} \frac{e^{x+h}-e^{x}}{h} \\ =\frac{\lim }{h \rightarrow 0} \frac{e^{x} \cdot e^{h}-e^{x}}{h} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times e^{x}\left(e^{h}-1\right) \\ =\frac{\lim }{h \rightarrow 0} \frac{e^{x}}{h} \times\left(1+h+\frac{h^{2}}{2 !}+\frac{h^{3}}{3 !}+-----1\right) \\ =\frac{\lim }{h \rightarrow 0} \frac{e^{x}}{h} \times h\left(1+\frac{h^{2}}{2 !}+\frac{h^{3}}{3 !}+--\right) \\ =\mathrm{e}^{x} \\ \therefore \frac{d}{d x}^{x^{x}}=e^{x} \end{array}$

(viii) $\frac{d}{d x}^{x^{n}}$ নির্ণয়ঃ

\begin{array}{l} \frac{d x^{n}}{d x}=\frac{\lim }{h \rightarrow 0} \frac{(x+h)^{n}-x^{n}}{h} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times\left[\left\{x\left(1+\frac{h}{x}\right)\right\}^{n}\right] \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times\left\{x^{n}\left(1-\frac{h}{x}\right)^{n}-x^{n}\right\} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times\left\{x^{n}\left(1-\frac{h}{x}\right)^{n}-x^{n}\right\} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times x^{n}\left\{\left(1-\frac{h}{x}\right)^{n}-1\right\} \\ =\frac{\lim }{h \rightarrow 0} \frac{x^{n}}{h}\left\{1+\frac{n h}{x}+\frac{n(n-1)}{2 !} \frac{h^{2}}{x^{2}}+\frac{n(n-1)(n-2)}{3 !} \frac{h^{3}}{x^{3}}+-----1\right\} \\ =\frac{\lim }{h \rightarrow 0} \frac{x^{n}}{h} \times \frac{n h}{x}\left\{1+\frac{(n-1)}{2 !} \frac{h}{x}+\frac{(n-1)(n-2)}{3 !} \frac{h^{2}}{x^{2}}+----\right\} \\ =n x^{n} \times \frac{1}{x}=n x^{n-1} \\ \therefore \frac{d}{d x}^{x^{n}}=n x^{n-1} \end{array}

(ix) $\frac{d}{d x}^{a^{x}}$ নির্ণয়ঃ

\begin{array}{l} \frac{d^{a^{x}}}{d x}=\frac{\lim }{\mathrm{h} \rightarrow 0} \frac{\mathrm{a}^{\mathrm{x}+h}-\mathrm{a}}{h} \\ =\frac{\lim }{\mathrm{h} \rightarrow 0} \frac{\mathrm{a}^{\mathrm{x}} \cdot \mathrm{a}^{\mathrm{h}}-\mathrm{a}^{\mathrm{x}}}{h} \\ =\frac{\lim }{\mathrm{h} \rightarrow 0} \frac{\mathrm{a}^{\mathrm{x}}\left(\mathrm{a}^{\mathrm{h}}-1\right)}{h} \\ =\frac{\lim }{\mathrm{h} \rightarrow 0} \frac{\mathrm{a}^{\mathrm{x}}}{h}\left\{1+h \ln a+\frac{h^{2}}{2 !}(\ln a)^{2}+\frac{h^{3}}{3 !}(\ln a)^{3}+----\quad-1\right\} \\ =\frac{\lim }{\mathrm{h} \rightarrow 0} \frac{\mathrm{a}^{\mathrm{x}}}{h} \times h \ln a\left\{1+\frac{h^{2}}{2 !}(\ln a)+\frac{h^{3}}{3 !}(\ln a)^{2}+----\right\} \\ =a^{x} \ln a \\ \therefore \frac{d}{d x} a^{x}=a^{x} \ln a \end{array}

(x) $\frac{d}{d x}^{\ln x}$ নির্ণয়ঃ

$\begin{array}{l} \frac{d}{d x} \ln x \\ =\frac{\lim }{h \rightarrow 0} \frac{\ln \left(\frac{x+h}{x}\right)}{h} \\ =\frac{\lim (x+h)-\ln x}{h \rightarrow 0} \frac{1}{h} \times \ln \left(1+\frac{h}{x}\right) \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times\left\{\frac{h}{x}-\frac{1}{2} \frac{h^{2}}{x^{2}}+\frac{1}{3} \frac{h^{3}}{x^{3}}-\frac{1}{4} \frac{h^{4}}{x^{4}}+----\right\} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times\left\{\frac{h}{x}-\frac{1}{2} \frac{h^{2}}{x^{2}}+\frac{1}{3} \frac{h^{3}}{x^{3}}-\frac{1}{4} \frac{h^{4}}{x^{4}}+----\right\} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times \frac{h}{x}\left\{1-\frac{1}{2} \frac{h}{x}+\frac{1}{3} \frac{h^{2}}{x^{2}}-\frac{1}{4} \frac{h^{3}}{x^{3}}+----\right\} \\ =\frac{1}{x} \\ \therefore \frac{d}{d x} \ln x \end{array}$

(xi) $\frac{d}{d x} \log _{a} x$ নির্ণয়ঃ

$\begin{array}{l} \frac{d}{d x} \log _{a} x=\frac{\lim }{h \rightarrow 0} \frac{\log _{a}(x+h)-\log _{a} x}{h} \\ =\frac{\lim }{h \rightarrow 0} \frac{\log _{a}\left(\frac{x+h}{x}\right)}{h} \\ =\frac{\lim }{h \rightarrow 0} \frac{\log _{a}\left(1+\frac{h}{x}\right)}{h} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times \log _{a} c \times \log _{c}\left(1+\frac{h}{x}\right) \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h} \times \frac{1}{\log _{c} a} \times \ln _{c}\left(1+\frac{h}{x}\right) \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h \ln a} \times\left\{\frac{h}{x}-\frac{1}{2} \frac{h^{2}}{x^{2}}+\frac{1}{3} \frac{h^{3}}{x^{3}}-----------\right\} \\ =\frac{\lim }{h \rightarrow 0} \frac{1}{h \ln a} \times \frac{h}{x}\left\{1-\frac{1}{2} \frac{h}{x}+\frac{1}{3} \frac{h^{2}}{x^{2}}-\right. \\ =\frac{1}{x \ln a}=\frac{1}{x} \times \frac{1}{\log _{c} a}=\frac{1}{x} \times \log _{a} c \\ \therefore \frac{d}{d x} \log _{a} x \\ =\frac{1}{x \ln a}=\frac{1}{x} \times \log a c \end{array}$

সূত্র (Formula) :

1. $\frac{d}{d x}^{\{c f(x)\}}=c \frac{d}{d x}^{f(x)}$ ; c = ধ্রুবক

2. $\frac{d^{c}}{d x}=0 ; \quad \mathrm{c}=$ ধ্রুবক

3. $\frac{d}{d x}^{(u+v)}=\frac{d}{d x}^{u}+\frac{d^{v}}{d x}$

4. $\frac{d}{d x}^{(u-v)}=\frac{d}{d x}^{u}-\frac{d^{v}}{d x}$

5. $\frac{d}{d x}^{(u v)}=u \frac{d}{d x}^{v}+v \frac{d}{d x}^{u}$

6. $\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{v \frac{d}{d x}^{u}-u \frac{d}{d x}^{v}}{v^{2}}$

এইচএসসি ও এডমিশন পরীক্ষার্থীদের জন্য আমাদের কোর্সসমূহঃ

আমাদের স্কিল ডেভেলপমেন্ট কোর্সসমূহঃ

১০ মিনিট স্কুলের ক্লাসগুলো অনুসরণ করতে ভিজিট: www.10minuteschool.com

Other Topics