স্পর্শ জ্যা এবং এর সমীকরণ | Equation of Chord of Contact

স্পর্শ জ্যা কাকে বলে?

কোনো বৃত্তের বহিঃস্থ একটি বিন্দু হতে বৃত্তে দুইটি স্পর্শক (tangent) অঙ্কন করা হলে যে স্পর্শ বিন্দুদ্বয় পাওয়া যায় তাদের সংযোজক সরল রেখাংশকে উক্ত বিন্দু হতে অঙ্কিত স্পর্শকের স্পর্শ জ্যা বলা হয়।

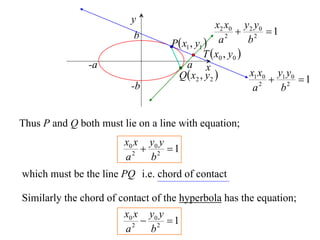
স্পর্শ জ্যা কাকে বলে?

$x^2+y^2=a^2$ বৃত্তের বহিঃস্থ $(x_1,y_1)$ বিন্দু হতে অঙ্কিত স্পর্শকের স্পর্শ জ্যা নির্ণয়:

মনে করি, $P(x_1,y_1)$ প্রদত্ত বৃত্তের বহিঃস্থ একটি বিন্দু এবং $PA$ ও $PB$ দুইটি স্পর্শক (tangent)। $A(x_2,y_2)$ এবং $B(x_3,y_3)$ বিন্দুদ্বয় স্পর্শ বিন্দু। তাহলে, $AB$ সরলরেখাংশই নির্ণেয় স্পর্শ জ্যা যার সমীকরণ (Equation) নির্ণয় করতে হবে।

এখন, $A$ বিন্দুতে স্পর্শকের সমীকরণ (Equation), $xx_2+yy_2=a^2$

$B$ বিন্দুতে স্পর্শকের সমীকরণ (Equation), $xx_3+yy_3=a^2$

স্পর্শদ্বয় $P(x_1,y_1)$ বিন্দু দিয়ে যায়,

\therefore x_1x_2+y_1y_2=a^2......(i) এবং x_1x_3+y_1y_3=a^2......(ii)

$(i)$ ও $(ii)$ নং হতে বলা যায়, $(x_2,y_2)$ এবং $(x_3,y_3)$ বিন্দুদ্বয়ের উভয়েই $xx_1+yy_1=a^2$ সরলরেখার ওপর অবস্থিত।

সুতরাং স্পর্শ জ্যা $AB$ এর সমীকরণ (Equation), $xx_1+yy_1=a^2$

অনুরূপে, দেখানো যায়, $x^2+y^2+2gx+2fy+c=0$ বৃত্তের বহিঃস্থ $(x_1,y_1)$ বিন্দু হতে অঙ্কিত স্পর্শকের স্পর্শ জ্যা এর সমীকরণ (Equation), $xx_1+yy_1+g(x+x_1)+f(y+y_1)+c=0$

অনুসিদ্ধান্ত (Conclusion):

$x^2+y^2=a^2$ বৃত্তটির জ্যা $(a,b)$ বিন্দুতে সমদ্বিখণ্ডিত হলে জ্যা এর সমীকরণ (Equation) $ax+by=a^2+b^2$

দুইটি বৃত্তের সাধারণ জ্যা-এর সমীকরণ (Determination of common chord of two circles):

দুইটি বৃত্ত পরস্পরকে দুইটি বিন্দুতে ছেদ করলে ছেদবিন্দু দুইটির সংযোজক রেখাংশকে এদের সাধারণ জ্যা (Common Chord) বলে। $A$ ও $B$ কেন্দ্র এবং $r_1$ ও $r_2$ ব্যাসার্ধবিশিষ্ট বৃত্ত দুইটি পরস্পরকে ছেদ করবে যদি এবং কেবল যদি $AB<r_1+r_2$ হয়।

মনে করি, দুইটি বৃত্তের সমীকরণ (Equation),

C_1=x^2+y^2+2g_1x+2f_1y+c_1=0\; এবং\\ C_2=x^2+y^2+2g_2x+2f_2y+c_2=0

এবং এরা পরস্পরকে $P(x_1,y_1)$ এবং $Q(x_2,y_2)$ দুইটি বিন্দুতে ছেদ করে।

সুতরাং এদের সাধারণ জ্যা $PQ$

$P(x_1,y_1)$ বিন্দুতে $x_1^2+y_1^2+2g_1x_1+2f_1y_1+c_1=0......(1)$

এবং $x_1^2+y_1^2+2g_2x_1+2f_2y_1+c_2=0......(2)\\ (1)-(2)\Rightarrow 2(g_1-g_2)x_1+2(f_1-f_2)y_1+(c_1-c_2)=0$

অনুরূপভাবে, দেখানো যায়, $Q(x_2,y_2)$ বিন্দুতে $2(g_1-g_2)x_2+2(f_1-f_2)y_2+(c_1-c_2)=0$

তাহলে, $P(x_1,y_1)$ এবং $Q(x_2,y_2)$ উভয় বিন্দুতেই $2(g_1-g_2)x+2(f_1-f_2)y+(c_1-c_2)=0 ......(3)$

সমীকরণকে সিদ্ধ করে এবং এটি একটি একঘাত সরল সমীকরণ (Equation) বলে একটি সরলরেখা নির্দেশ করে।

সুতরাং (3) নং সমীকরণটিই $P(x_1,y_1)$ এবং $Q(x_2,y_2)$ বিন্দু দুইটির ছেদবিন্দুগামী সরলরেখার সমীকরণ (Equation) এবং বৃত্ত দুইটির সাধারণ জ্যা -এর সমীকরণ (Equation)।

আবার বৃত্তের সমীকরণ (Equation) দুটি বিয়োগ $(C_1-C_2)$ করে পাই, $2(g_1-g_2)x+2(f_1-f_2)y+(c_1-c_2)=0$ যা $(3)$ নং সমীকরণের সাথে অভিন্ন।

সুতরাং বৃত্ত দুইটির সমীকরণ (Equation) বিয়োগ করে তাদের সাধারণ জ্যা এর সমীকরণ (Equation) পাওয়া যায়।

সুতরাং $C_1=0$ এবং $C_2=0$ সমীকরণ (Equation) বিশিষ্ট দুইটি পরস্পরছেদী বৃত্তের সাধারণ জ্যা- এর সমীকরণ (Equation), $C_1-C_2=0$

অনুসিদ্ধান্ত (Conclusion):

যদি দুটি বৃত্তের সাধারণ জ্যা $L=(c_1-c_2)=0$ হয়, তবে বৃত্ত দুটির ছেদবিন্দুগামী বৃত্তের সমীকরণ (Equation) হবে,

$C_1+KL=0$
$C_2+KL=0$
$C_1+KC_2=0$

এখানে $K$ একটি ধ্রুবক যার মান বৃত্তদ্বয়ের ছেদবিন্দু থেকে পাওয়া যাবে।

এইচএসসি ও এডমিশন পরীক্ষার্থীদের জন্য আমাদের কোর্সসমূহঃ

আমাদের স্কিল ডেভেলপমেন্ট কোর্সসমূহঃ

১০ মিনিট স্কুলের ক্লাসগুলো অনুসরণ করতে ভিজিট: www.10minuteschool.com

Other Topics